序型·序数

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第69页（1086字）

集合的形如(a，b)的元素称为有序对。

如果一集合的每一个元素都是有序对，则称这个集合为关系。如果R是一个关系，我们常将(a，b)εR写成aRb。

称关系R是集合A上的偏序关系，如果下列条件对于x，y，z属于A成立：

(1)自反性 xRx

(2)反对称性 xRy∧yRx→xRy

(3)可传递性 xRy∧yRz→xRz

如果R在A上还是连通的，即对于任意的x，yεA，均有xRy∨yRx，则称R是A上全序关系。

并称(A，R)是一个序结构，当R是明确的或不必提及时，也说A是一个全序集。

称序结构(A，R)，(B，S)是相似的，如果存在A到B上的双射f，并且f还保持序关系：对任意x，yεA，有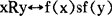

易于验证，序结构之间的相似关系是一个等价关系。因此，可将所有的序结构分成等价类。

每个序结构所在的等价类都有一种特征性质，这个特征性质称为这个等价类的元素的序型。我们用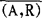表示序结构(A，R)的序型，有时也用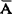表示全序集A的序型。序结构(A，R)，(B，S)的序型是相同的，如果存在由A到B上保序的双射。

将集合排序后，我们便可以比较集合的元素之间的大小了。相应地便有最大元、最小元，极大元，极小元的概念。

A的元素a称为序结构(A，R)的R极大(小)元，如果对于任意的A中不等于a的元素b，aRb(bRa)不成立。

A的元素a称为序结构(A，R)的R最大(小)元，如果对于任意的b属于A，均有bRa(aRb)。

设(A，R)是一序结构，如果对于A的任意非空子集B，B均有R最小元(即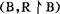有最小元)，则称(A，R)是良序结构。

良序结构有许多非常好的性质，人们对这样的序结构进行了深入的研究。

良序结构的序型称为序数。康托还定义了序数上的算术运算术，这里就不详述了。