基数
出处:按学科分类—自然科学总论 山东人民出版社《方法大辞典》第87页(1175字)
对集合进行研究的一个重要方面是研究集合中元素的多少,集合的基数便是用来衡量集合中元素的多少的。
为了比较两个集合的元素的多少,我们还需引进集合等价的概念。
如果存在从集合A到集合B上的1-1函数,则称A与B是等价的,或称A与B等势。显然,我们有:(1)A与A等价;(2)如果A与B等价,则B与A等价;(3)如果A与B等价并且B与C等价,则A与C等价。因此,我们可以按此等价关系将集合分成一些两两互不相交的类,使每个集合都属于某个类,并且集合A与B在同一类中当且仅当A与B等价。
上述分类中的每一类都有自己的一种特征性质,根据这个特征性质,决定一个集合是否属于这个类。我们把集合A所在的类的特征性质称为A的基数,并用|A|表示它。
上面关于集合基数的描述并不是严格的数学定义,但这并不影响理论的发展。事实上,我们只要求基数满足下面这个式子便行了:
|A|=|B|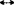 存在从A到B上的1-1函数。
存在从A到B上的1-1函数。
我们说A的基数小于或等于B的基数,如果A与B的某个子集的基数相等,用符号表示为|A|≤|B|。如果|A|≤|B|并且|A|≠|B|,则称A的基数小于B的基数,记为|A|<|B|。
基数的许多性质与我们熟悉的有穷集的元素的个数的性质相同,基本的有:
(1)|A|=|A|
(2)|A≤|B|∧|B|≤|A|→|A|=|B|
(3)|A|≤|B|∧B|≤|C|→|A|≤|C|
(4)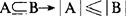
基数也有些与有穷集的元素的个数性质不同的性质。比如,一个集合的基数可以与它的一个真子集的基数相等。
我们用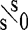 (阿列夫零)表示自然数集的基数,用
(阿列夫零)表示自然数集的基数,用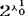 表示实数集的基数。康托证明了下面的不等式
表示实数集的基数。康托证明了下面的不等式
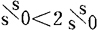
康托自己一直没有找到基数大于s/s0并且小于2s/s0的集合。他提出猜想:这样的集合是不存在的。这便是着名的连续统假设。
后来,人们证明了这个假设与通常的集论公理是独立的。
康托还定义了基数的算术运算它是自然数的算术运算的推广。