演绎方法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第108页（1481字）

亦称演绎，它译自拉丁文deductio，意为“引伸”，是从一般引伸出特殊的过程。

演绎方法包括演绎推理和以演绎推理为基础的证明和公理方法。

演绎推理是前提与结论之间具有蕴涵关系的推理，或者说，前提与结论之间具有必然联系的推理。

例如：

(1)所有的哺乳动物都是脊椎动物，所有的反刍动物都是哺乳动物，所以，所有的反刍动物都是脊椎动物。

(2)只有能被3整除的数，才能被6整除，18能被6整除，所以，18能被3整除。

这虽然是两个不同的推理，但它们都是前提与结论之间具有必然联系的推理，即有蕴涵关系的推理。它们的推理形式分别是：

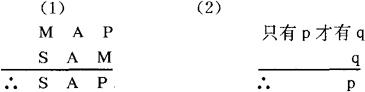
在推理形式(1)中，不论以任何概念代入“S”与“P”，或者在推理形式(2)中，以任何判断代入“p”与“q”，只要代入后的前提是真实的，那么，代入后的结论一定是真实的。这就说明在演绎推理中，从真实的前提出发，运用有效的推理形式，就必然得出真实的结论。

公理方法是一种重要的演绎方法。

它是从一些称作公理的命题出发，根据演绎推理规则，推导出一系列定理，从而构成一个演绎体系。

这种体系叫做公理系统，欧氏几何就是一个古典的公理系统。

欧几里得在《几何原本》中列出五条公设和五条公理，并从这些公设和公理出发，推出几何学的所有定理。当一个理论发展到成熟阶段，如同欧几里得时代的几何学，人们总要安排这门学科的逻辑体系，从甲概念定义出乙概念，又从乙概念定义出丙概念，从甲定理推出乙定理，又从乙定理推出丙定理。

这样的排列，使人容易掌握该学科中每个概念，每个定理之间的逻辑关系。欧氏把几何中的所有概念都下了定义，一切定理都作了证明，得出一个严格的几何系统。

当然，不可能对一切判断都加以证明，开头时必有几条原理是不能证明也无需证明的，这就是公理。同样，要想对一切概念都加以定义也是不可能的，开头时必有几个概念是无法定义的，这就是初始概念，用初始概念来定义所有的其余概念，有了公理和初始概念以后，所研究的学科中的一切概念便都可以定义了，学科中一切成立的命题便都可以证明为定理了。

列出初始概念与公理，从而对一切概念给以定义，对一切定理给以证明，这种方法就叫做公理方法。

数学、力学理论科学等已经普遍地使用了公理方法，取得巨大的成就，其他比较成熟的学科，也都朝着采用公理方法的方向前进。

假说演绎法是以假设作前提来解释科学探索中所需要解释的东西。它比单纯的归纳或单纯的演绎更符合创造性思维的实际情况。

演绎方法不能单独地被应用于科学思维中，必须与其他的逻辑方法，如归纳、类比、假设等结合起来应用，才能达到科学发现的目的。

“归纳和演绎，正如分析和综合一样，是必然相互联系着的，不应当牺牲一个而把另一个捧到天上去，应当把每一个都用到该用的地方，而要做到这一点，就只有注意它们的相互联系、它们的相互补充。”(《马克思恩格斯选集》第3卷第548页)