线性规划
书籍:方法大辞典
出处:按学科分类—自然科学总论 山东人民出版社《方法大辞典》第123页(600字)
一般表述为选择某些非负值的变量,在满足线性函数的不等式或等式的条件下,使某一线性函数的目标值达到最大或最小的方法。
最早研究这个问题的是苏联的数学家П.в.康脱洛维奇,他于1939年写了《生产组织与计划中的数学方法》一书,后来美国的G.B.丹茨基又于1947年提出线性规划问题的一般性模型和方法——单纯形法。从那时起正式出现了线性规划这个名称,并成为独立的数学分支。
线性规划问题的数学模型:
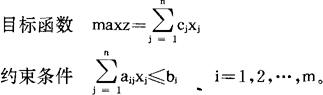
Xj≥0 j=1,2,…,n。
其中ai、bi和cj是已知常数,xj为非负变量,z是xj的函数。
线性规划的运算方法有经验试凑法,图解法,表上作业法,单纯形法等。其中应用较为普遍的是单纯形法。单纯形法的理论根据是对于任一有解存在的线性规划问题,它的可行解组成的凸多面体的顶点数是有限的,且其最优解必在其中的某一顶点上。因此,求解一个线性规划问题只要算出每个顶点处目标函数的值,然后从中选出最大(或最小)值。
单纯形法运算步骤是先求出一个能够符合所有约束条件的可行解,然后用迭代方法,求得目标函数的极大或极小值。