估计标准误差

出处：按学科分类—社会科学总论 上海人民出版社《统计辞典》第338页（768字）

亦称“标准估计误差”。

指根据回归方程由自变量(x)数值推算出因变量(y)数值所产生的误差。由于从回归方程推出的因变量的数值并不是精确的数值，而是估计值或平均值，它和真正的实际值有出入。如果其出入很小，说明推算的结果准确程度高；反之，则准确程度就低。换句话说，这个差别大小也反映回归直线的代表性大小。

估计标准误差就是用来说明回归方程推算结果的准确程度，或者是反映回归直线代表性大小的指标。

估计标准误差的计算公式为：

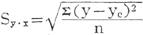
式中：S_y·x为估计标准误差，y为因变量数列的实际值，y_。为根据回归方程推算出的估计值，n代表因变量的项数。

上面计算的公式含义明显，但计算较繁。如果已有直线回归方程的参数值，可按下式计算。

y_c=a+bx

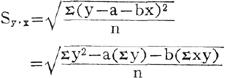
估计标准误差的作用在于它的数值大小反映了利用回归直线进行估计或预测的准确程度。估计标准误差大，则回归直线的代表性小，其实用价值也小；反之，代表性大，实用价值也大。

相关系数和估计标准误差之间有一定的关系，以公式表示：

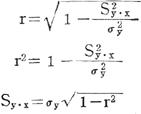
两者关系为：r值愈大，说明相关程度愈密切，这时S_y·x值愈小，相关点距回归直线较近。

当r=±1，则S_y·x=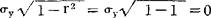，说明所有相关点都在回归直线y_c上，这就是完全正相关。反之，如r值愈小，表明相关不密切，则S_y·x值愈大，相关点距回归直线较远，当r=0即无相关时，则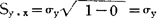，这表示相关点的x值不管怎样变化，y_c值始终不变，并等于y数列的平均值，这就不存在相关关系。