贝叶斯方法

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第284页（767字）

贝叶斯方法对于模型中参数的估计，不同于通常意义下的统计推断，它把模型中待估的未知参数看做随机变量而不是常数。

为了估计参数值，它首先假定分析者对这些参数有某种先验判断，而且这种判断能用概率形式表达出来，然后将先验概率同从实际样本观测得来的信息合并起来，以得到这些参数的后验概率。实际应用时，确定一种损失函数，再按照所得的后验概率分布，求出一个使平均损失最小的参数估计值。

这个估计值不再是随机变量，而是随机变量在某种意义下的最优值。

设有m个总体G₁，G₂，…，G_m，概率密度函数分别为f_i(x)，i=1，…，m，来自总体G_i的样品x被错判为来自总体G_j(i，j=1，…，m)时所产生的损失记为C(j|i)，并且C(i|i)=0，那么，如果记判别规则R=(R₁，R，…，R_m)产生误判的概率为P(j|i，R)，有

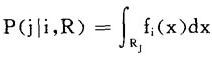
如果已知样品x来自总体G_i的先验概率为q_i(i=1，…，m)，则在规则R下，误判的平均损失为：

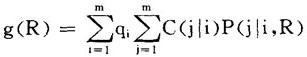
使g(R)最小的R为：

R_k={x|h_k(x)=minh_j(x)}，k=1，…，m其中

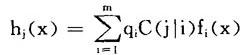
当多个参数(即样品x为向量)待估时，就需要先验地给出它们的多维分布。

为了能够准确地刻画后验分布，先验分布的选择既要易于化简，又要符合人们对参数的先验认识。这使得贝叶斯方法的实际应用，面临很大的局限性。