无理数

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第46页（309字）

无限不循环小数。

它是在解决不可公度线段比的矛盾过程中产生的。例如，边长为1的正方形对角线长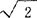就是不可公度的量，圆的直径与圆之比π=3．1415926……也是不可公度的量即无理数。

有了无理数，开方开不尽的矛盾得到了解决。

无理数与有理数是对立统一的，人们认识无理数是由有理数转化而来的。

无理数并非绝对的“无理”，它与有理数在一定条件下可以相互转化，在实际计算中，有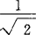===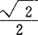0．71；解无理方程时也把它转化成有理方程；无理数可用有理数逼近到任意精度等。无理数与有理数全体组成实数系。

它使数与直线上的点建立起一一对应关系，把具有连续性的线看成点的集合，用数表示量达到了精确的程度。