导函数

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第364页（566字）

微分学中的一个重要概念。

设x是函数y=f(x)定义域中的一点，对于给定的一点x₁，函数值的改变量f(x₁)－f(x)记作△y，x的改变量x₁－x记作△x。当△X→0时，若改变量之比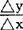的极限存在，则称此极限为f(x)在点x的导数，记作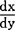或f′(x)。当x为变动点时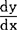，便是x的导函数。它在数学、物理、工程技术等方面有着广泛的应用。例如，在变速运动中，路程S是时间T的函数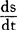，表示运动物体在时刻t的瞬时速度。在几何上，f′(x)表示曲线y=f(x)在点(x，y)的切线的斜率。实际上导函数的产生是17世纪一些有名的数学家致力于曲线切线问题讨论的结果。现用的符号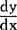是由莱布尼茨提出来的，但他本人也是含糊不清。

马克思对导函数的生成过程作了辩证的分析。他认为，导函数的生成过程，确是变数运动、变化，并经历了“否定之否定”的发展过程。根据这种分析，高等数学中几乎所有的证明，从初等数学的观点看来严格地说都是错误。导函数的这种辩证性质，显示了只有微分学才能使自然科学有可能用数学来不仅仅表明状态，并且也表明过程、运动。

马克思还对导数符号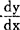的意义作了深刻的阐述，认为只有把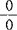中质的关系同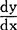固定下来，才有可能去确定那些与一阶导函数不同的而又与它们相联系并且从中产生出来的各阶导函数，并指出这里的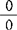是一个完全确定的形式。