纯代数的微分学

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第460页（571字）

马克思在《数学手稿》中评述微分学奠基问题时对拉格朗日力图把微分学代数化思想的一种代称。

拉格朗日以增长了的x，如x₁=x+h，并用纯代数的方法将f(x+h)展开成幂级数作为自己的直接出发点，然后大造术语，即把展开式中各项的有关系数称作各阶导函数。例如，用纯代数方法将f(x+h)展开成幂极数：f(x+h)=f(x)+a₁h+a₂h²+……+a_nhⁿ+o(hⁿ)，于是，称a₁为一个阶导函数，zla₂为二阶导函数，nlan为阶导函数。马克思对拉格朗日这种思想方法进行了深刻的分析。

他说：“为了把微分学代数化，拉格朗日就用牛顿派和牛顿见到了的泰勒的那个定理作为他直接的出发点，实际上这就是最一般的最概括的定理，同时也是微分学的运算公式，亦即用符号微分系数表示的y₁或f(x+h)的展开级数”(《数学手稿》第93页)。

就是说，泰勒定理本来是用导函数概念证明了的一个概括性定理和运算公式，即“若f(n)(x)存在，当h→o，则f(x+h)=f(x)+f′(x)h+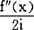h²+……+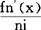hⁿ+o(hⁿ)”。可是，拉格朗日却作为自己的直接出发点，拿过来就起名字，因此他犯了一个逻辑循环的错误，当然更谈不上揭示微分学的实质了。

马克思在《数学手稿》中，对拉格朗日在微分学奠基问题研究上所作出的贡献，也给予了充分的肯定。