神秘的微分学

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第659页（890字）

马克思在《数学手稿》中评述微分学奠基问题时对牛顿和莱布尼茨建立起来的微分学的一种称呼。

牛顿和莱布尼茨在从原函数推导导函数的过程中，一开始就把变量的增量当作微分，即x+△x=x+dx，y+△y=y+dy(莱布尼茨用dx，dy，牛顿用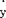，)，然后，通过强制抹去一些项而获得导函数。例如，设原函数为y=f(x)=x³，x的增量为dx，y的增量为dy，于是y+dy=(x+dx)³=x³+3x²dx+3xdx²+dx。因为y=x³，所以dy=3x²dx+3xdx²+dx³。这时，抹掉3xdx²和dx³，得dy=3x²dx，从而dy／dx=3x²。马克思对牛顿和莱布尼茨的这种求导函数的方法，从哲学上进行了深刻的分析，并着重揭示其形而上学和先验主义的实质。首先，马克思指出：“x₁=x+△x从一开始就变成x₁=x+dx或x+x，这里dx是通过形而上学的解释假定的。”(《数学手稿》第85页)“先验地假定dx，dy等等或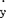，等等作为x和y的独立和孤立的增量”(《数学手稿》第99页)。其次，马克思又指出，消去3xdx²和dx³是采取了“用魔术变掉”、“暴力镇压”的手法；“这种算法通过肯定是不正确的数学途径得出了正确的(尤其在几何应用上是惊人的)结果。

”(《数学手稿》第88页)最后，马克思对牛顿和莱布尼茨的微分学及其引起的争论做了概括，指出：“于是，人们相信了新发现的算法的神秘性。……人们就这样把自己神秘化了，对这新发现评价更高了，使一群旧式正统派数学家更加恼怒，并且激起了敌对的叫嚣，这种叫嚣甚至在数学界以外产生了反响，而为新事物开拓道路，这是必然的。

”(《数学手稿》等88页)事实上，牛顿和莱布尼茨的神秘微分学，不仅在数学领域中遭到了正统派数学家的反对，引起了数学界的混乱，导致关于数学基础研究的第二次危机，而且还在哲学界中遭到了主观唯心主义者贝克莱的攻击，他说微积分包含“大量的空虚、黑暗和混乱”，是“分明的诡辩”。但是，这种神秘的微分学，在实践的推动下，在学术争论以及两种哲学思想的斗争过程中，不断克服其神秘性，逐步完善和发展起来。