理性的微分学

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第761页（686字）

马克思在《数学手稿》中评述微分学奠基问题时对达兰贝尔微分学的一种称呼。

达兰贝尔修正了牛顿和莱布尼茨的求导方法，首先给自变量x以有限增量△x=h，函数y=f(x)以相应的有限增量为△y，并构成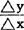，然后令h=0推得导函数。例如，设y=f(x)=x³，△x=h(≠0)，△y=f(x+h)－f(x)，因为f(x+h)=(x+h)³=x³+3x²h+3xh2+h³，所以△y=3x²h+3xh²+h³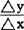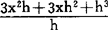，==3x²+3xy+h²，这时令h=0，则3xh+h²=0，故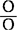==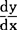3x²。

马克思对达兰贝尔的这种方法作了深刻的哲学分析。首先指出这种方法比牛顿、莱布尼茨方法有所前进，一方面“通过设h=0，就是说通过正确的数学运算，3xh+h²这两项也都变为0了。因此，现在不用变摩术，就把它们取消了。”(《数学手稿》第90页)另一方面，△x向dx“的转化只是作为发展的最后或至少是接近末尾的结果”(《数学手稿》第88页)。而牛顿和莱布尼茨却把dx作为直接的出发点，所以“达兰贝尔脱下了微分学的神秘外衣，取得了很大的进步。”(《数学手稿》第91页)其次，马克思又揭露了达兰贝尔方法的形而上学实质，指出：“这个完全现成的导数3x²是用严格的代数法从它的其他联系中解脱出来的。这不是发展，仅仅是把f′(x)，即这里的3x²，从它的因子h以及从与它并列的其他各项中解脱出来而已。

而真正发展了的，是左边，即dx、dy及它们的比，即符号微分系数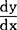=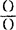(不知反过来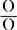=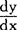)，这个符号虽然是由数学推导出来的，但又引起过某些形而上学的恐怖”(《数学手稿》第90－91页)。