模糊子集
书籍:自然辩证法辞典
更新时间:2018-11-17 06:11:08
出处:按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第909页(546字)
模糊数学中的基础概念。
指给定了论域U上的一个模糊子集A,对于任意u∈U,都指定一个称之为u对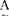 的隶属程度的数UA(u)∈[0,1]。映射μA:U→[0,1]叫作A的隶属函数。模糊子集完全由其隶属函数所刻划,当μ
的隶属程度的数UA(u)∈[0,1]。映射μA:U→[0,1]叫作A的隶属函数。模糊子集完全由其隶属函数所刻划,当μ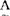 的值域={0,1}时,A便蜕化成一个普通子集,μ
的值域={0,1}时,A便蜕化成一个普通子集,μ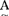 X为其特征函数。于是,设∮(U)和
X为其特征函数。于是,设∮(U)和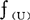 分别为U上的全体普通子集和全体模糊子集所构成的类,则有:
分别为U上的全体普通子集和全体模糊子集所构成的类,则有: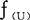
 ∮(u)且当
∮(u)且当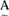 ∈
∈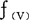 -∮(U)时,
-∮(U)时,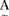 叫作真模糊子集。
叫作真模糊子集。
当论域U有限时,设U={a1,a2,……an},则U上的一个模糊子集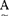 表为:
表为: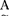 =μ
=μ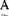 (a1)/a1+μA(a2)/a2+……+μA(an)/an当论域U是无限时,使用记号
(a1)/a1+μA(a2)/a2+……+μA(an)/an当论域U是无限时,使用记号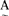 =∫(μA(u)/u)来表示U上的一个模糊子集A,当然,表示的方法还有许多,并且各有优点。模糊子集的运算较多地是采用扎德给出的定义:设
=∫(μA(u)/u)来表示U上的一个模糊子集A,当然,表示的方法还有许多,并且各有优点。模糊子集的运算较多地是采用扎德给出的定义:设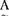 ,
,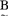 ∈F(U),定义
∈F(U),定义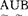 (并),
(并),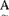 nB(交),
nB(交),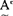 (余)分别具有下列隶属函数:
(余)分别具有下列隶属函数: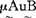 (u)
(u)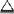 max(
max(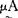 (u),
(u), (u)),μAB(u)
(u)),μAB(u)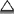 min(μA(u),
min(μA(u),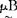 (u),
(u),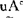
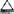 1-
1-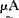 (u)。可以证明,普通集合运算的不少性质,对模糊集合也仍然适用。模糊数学从1965年发展至今,发展速度很快,应用的触角正伸向科技领域的许多方面。
(u)。可以证明,普通集合运算的不少性质,对模糊集合也仍然适用。模糊数学从1965年发展至今,发展速度很快,应用的触角正伸向科技领域的许多方面。
而作为模糊数学之基础的模糊子集自然有很大的作用,并占有很重要的地位。