射影几何

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第715页（558字）

数学的一个分支学科。

起端于欧洲文艺复兴时期透视学的研究。从19世纪开始得到蓬勃的发展。主要先驱者是17世纪法国的笛沙格(Desargns，G·)和帕斯卡(Pasсua，B．)。

首先给出系统严密论述的是19世纪法国的彭色列(Poncelet，J．)。

这种几何主要研究在把点投射到直线或平面上时，图形的不变的性质。在射影几何里，图形保持不变的最基本性质是点与直线的结合性，即在每一个中心投影之下，点与直线的位置关系保持不变。最基本的不变量是交比，即在它所论及的两组图形之间确定了一个保持交比的一一对应。例如，设P_i，P_i′(i=1，2，3，4)是两直线上对应的点，x_i，x_i′(i=1，2，3，4)是它们相对应的坐标，则关系式

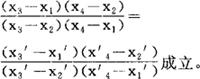
这种几何有两个明显特点：(1)引入一条理想直线，每一条通常的直线都与它相交，相互平行的直线交于同一点。

(2)对偶原理，把每一个命题中所包含的概念换上与它对偶的概念，相应的命题也成立。例如，“直线”与“点”是对偶的元素。在射影几何里，不存在距离、角度、面积、体积、向量、平行和分点等观念，因为它们在中心投射下是要改变的。因此，它和欧氏几何相比，范围最大，内容却最少。

欧氏几何是射影几何的子几何。