BCK－代数的理想

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第19页（3794字）

BCK代数作为一个抽象代数系统，当其初等理论建立以后，如何引入它的理想，就成为BCK－代数深入发展的一个关键问题。

1975年日本井关清志引入了BCK－代数的理想概念，充分反映了BCK－运算*的不对称性这一特点。多年的发展表明，理想理论是BCK－代数的最重要最基本的理论分支之一，与格论，环论和布尔代数等有着广泛的联系，它的出现标志BCK代数的研究进入新的阶段。

BCK－代数＜X；*，0＞的非空子集I叫做理想，如果它满足：0∈I和x*y，y∈I蕴涵x∈I。

以I(X)记X的全体理想之集，显然｛0｝，X∈I(X)。

如果I(X)=｛｛0｝，X｝，则称X是单的。包含子集A的最小理想称为A生成的理想，记为(A〕。如果A是有限集，则称(A〕是有限生成的。代数学的一个重要问题是：如何用A表示(A〕。

井关清志给出了一个优美的结果：u∈(A〕当且仅当存在x₁，…，x_n∈A使(…(u*x₁)*…)*x_n=0。以该结果为工具，波兰T．特拉塞科(T．Traczyk)和M．帕兰辛斯基(M．Palansinski)先后证明＜I(X)，∈＞是一个无限分配格，即，I₂∈I(X)，I₁∩I₂是含于I₁和I₂的最大理想，(I₁∪I₂〕是包含I₁和I₂的最小理想；，J_α∈I(X)(α∈A)，I∩(∪｛J_α：α∈A｝〕=(∪｛I∩J_α：α∈A｝〕。

理想的重要作用之一是构造商代数。对于BCK－代数X的理想I，称x～y当且仅当x*y，y*x∈I。

二元关系～是X上的一个同余关系，以C_x记包含x的等价类，定义C_x*C_y=C_x*y，则＜X／I；*，I＞是一个BCK－代数，其中X／I=｛C_x：x∈X｝，称做X关于I的商代数。巴基斯坦阿汗山(J．Ahsan)和德赫木(A．B．Thaheem)证明了对应定理：以〔I，X〕表示X中包含I的所有理想之集，则映射μ：〔I，X〕→I(X／I)使得μ(J)=J／I是一个格同构。由对应定理知，理想I是极大的当且仅当X／I是单的。

用理想刻划代数是BCK－代数中一个有趣的研究方向。

井关清志和田中昭太郎(S．Tanaka)最初引入两类代数：正定关联BCK－代数和每个理想是正定关联的BCK－代数。这两类代数有何关系?经过3年多的研究，1979年井关清志证明它们是等价的。从而开创了用理想刻划代数的研究方向。孟杰于1986年引入关联理想概念，借此刻划了关联BCK－代数。

如何引入可换理想，并借以刻划可换BCK－代数?这里存在的主要困难是x*(x*y)和y*(y*x)在一般BCK－代数中关于BCK－序≤不可比较，而可换性条件是x*(x*y)=y*(y*x)。为了克服这一困难，孟杰从寻找可换性等价条件着手，1988年证明可换性等价于：x≤y蕴涵y*(y*x)=x。借此引入了可换理想的概念，并研究以上3类理想的分布状态。BCK－代数X的非空子集I叫做一个正定关联理想，如果它满足：0∈I和(x*y)*z，y*z∈I蕴涵x*z∈I。

I叫做一个可换理想，如果它满足：0∈I和(x*y)*z，z∈I蕴涵x*(y*(y*x))∈I。I叫做一个关联理想，如果它满足t0∈I和(x*(y*x))*z，z∈I蕴涵x∈I。一个理想是关联的当且仅当它既是可换的又是正定关联的。关于它们的分布状态有下述深刻结果：设I和J是X的两个理想，且，如果I是正定关联(可换，关联)理想，则J也是正定关联(可换，关联)理想。

用理想可以刻划代数：BCK－代数X是正定关联(可换，关联)的，当且仅当X的每个理想是正定关联(可换，关联)的当且仅当零理想｛0｝是正定关联(可换，关联)的。理想理论的发展推动了商代数研究的深入：若I是BCK代数X的一个理想，则X／I是可换(正定关联，关联)的，当且仅当I是一个可换(正定关联，关联)理想。特别地，I既是极大的又是关联的当且仅当X／I是二阶BCK－代数。这是布尔代数中Tarski定理的推广：布尔代数X的理想I是极大的当且仅当。

理想的分解是理想理论的另一个研究方向。阿汗山开创了这个方向。BCK－代数X叫做一个诺德(Noether)代数，如果它的每个理想是有限生成的。理想I叫做既约的，如果，B∈I(X)，A∩B=I蕴涵A=I或B=I。

1977年阿汗山得到了既约分解定理：若X是一个诺德代数，则它的每个理想是有限多个既约理想的交。他在有界关联BCK－代数条件下得到了质分解定理，由于有界关联BCK－代数是布尔代数，所以阿汗山的质分解定理实质上是布尔代数相应结果的平移。为了减弱有界关联的条件，必须揭示BCK－代数的特性。帕兰辛斯基给出下述重要引理：在BCK－下半格X中，如果对自然数m和n有a*ⁿx=a*^my=0，则存在自然数k使得a*^k(x∧y)=0，其中x∧y=inf｛x，y｝，x*¹a=x*a，a*ⁿx=(a*^n－1x)*x，这为他的质分解定理打下了基础。

BCK－下半格X中的理想I叫做质的，如果x∧y∈I蕴涵x∈I或y∈I。帕兰辛斯基于1982年得到质分解定理：若BCK－下半格X是一个诺德代数，则它的每个理想是有限多个质理想的交。

他还讨论了极小质分解及唯一性的问题。质理想和商代数的关系，以1991年阿汗山(J．Ahsan)、迪巴(E．Y．Deeba)、德赫木(A．B．Thaheem)下述结果为最好：可换BCK－代数X的理想I是质的当且仅当X／I满足消去律，即C_x∧C_y=C₀蕴涵C_x=C₀或C_y=C₀。迪巴还证明在适当的运算下，I(X)是一个BCK－代数。

理想与同态是密切相关的。若＜X；*，0＞和＜Y；*，0＞是BCK－代数，映射f：X→Y叫做一个同态映射，如果，b∈X，f(a*b)=f(a)*f(b)。集合Ker(f)=｛x∈X：f(x)=0｝叫做f的核。

井关清志证明Ker(f)是X的一个理想。如果f还是满射，则，这就是第1同构定理。

中国黄涵和黄俊敏分别建立了第2和第3同构定理，后者还系统研究了BCK代数的根性。

1987年美国古尔(S．K．Goel)和阿罗拉(A．K．Arora)考虑如下问题：设I是X的一个理想，Y是任一个BCK－代数，存在同态映射f：X→Y使得Ker(f)=I吗?显然回答是否定的。

那么当I附加何种条件时，回答是肯定的?为解决这一问题，他们引入了固执理想的概念。理想I叫做固执的(obstinatl)，如果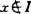和蕴涵x*y∈I。

他们证明：若X和Y是任意两个BCK－代数，I是X的一个固执理想，则存在同态映射f：X→Y使得Ker(f)=I。1992年孟杰证明这个结论的逆也成立。

井关清志、古尔、阿罗拉、帕兰辛斯基、孟杰等讨论了各种理想的关系：在一般的BCK－代数中，固执理想、极大且关联的理想、极大且正关联的理想彼此等价；固执理想必是既约理想，但其逆不真。

在BCK－下半格中，既约理想等价于质理想。

在关联BCK－代数中，固执理想、极大理想、质理想和既约理想彼此等价。

BCK－代数是一个年轻的学科，它的理想理论远未成熟，今后将有更大的发展，下列问题将引起关注：(1)用格理想的观点和方法研究理想，加拿大胡章成(C．S．Hoo)和印度的罗马纳莫尔特(P．V．Ramana Murty)于1987年证明了有界可换BCK－代数中的理想必是格理想，其逆不真。

进一步关系有待研究。(2)1991年巴斯坦阿斯拉木(M．Aslam)和德赫木引入零化子、零因子和对合理想等概念，这些有待深入研究。(3)理想和同态是密切相关的。随着范畴论的观点方法渗入BCK－代数，势必对理想作广泛的研究。

(4)借鉴斯东(M．H．Stone)关于布尔代数和布尔环的工作。讨论BCK－代数的拓扑及其它分析问题。

。【参考文献】：

1 Iseki K.Tanaka S. Math,Japon,1976,21:351～366

2 Palansinski M. Math,Seminar Notes,1982,10:467～471

3 GoelSK, Arora A. K Math,Japon,1987,32:559～567

4 孟杰.数学年刊．1987,2: 262～268

5 孟杰.纯粹数学和应用数学,1990,6(2):33～37

6 Ahsan J, Deeba E Y , Thaheem A B. Math, Japon, 19.91, 36:875～882

7 AslamM , Thaheem A B. Math,Japon,1991,36:895～706

(西北大学孟杰教授撰)