拟常曲率流形
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第77页(4221字)
也称拟常曲率空间。
设M是一个n(>3)维黎曼流形,a和b是M上的两个函数,Z=ωiai是M上的一个向量场,如果M的曲率张量K具有形式
Khijl=a(ghjgil-ghlgij)+b(ghjωiωl+gilωhωj-ghlωiωj-gijωhωl) (1)
其中g是M的Riemann度量,则称M为拟常曲率流形。简记其为Q流形。并称Z为其生成元。当<Z,Z>=e时,(1)式中的 ,
, ,这里R是M的数量曲率,T是Z对应的Ricci主曲率。
,这里R是M的数量曲率,T是Z对应的Ricci主曲率。
当<Z,Z>=0时,称M为广义拟常曲率流形。这时函数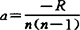 ,b不确定。亚射影流形和k特殊共形平坦流形均为特殊的拟常曲率流形。特别,当b=0时,Q流形便成为熟知的常曲率流形。
,b不确定。亚射影流形和k特殊共形平坦流形均为特殊的拟常曲率流形。特别,当b=0时,Q流形便成为熟知的常曲率流形。
如所知,常曲率流形既是共形平坦的,又是爱因斯坦的,即为特殊的共形平坦黎曼流形。介乎常曲率流形和共形平坦流形之间的黎曼流形的存在性问题,由T.Adati最早解决。1951年发表的《关于亚射影空间》的论文中,他指出了由B.Kagan和P.Rachevsky于1930年各自引入的“亚射影空间”是共形平坦的,并且证明亚射影空间是容有保圆变换的共形平坦空间;而使这类空间具有常数截面曲率的充要条件是

若从集合概念的角度去考察,这一结果表明,集合{共形平坦流形} {亚射影流形}
{亚射影流形} {常曲率流形}。因此,从20世纪30年代开始至60年代,有关亚射影流形的研究是几何学研究中活跃的课题之一。
{常曲率流形}。因此,从20世纪30年代开始至60年代,有关亚射影流形的研究是几何学研究中活跃的课题之一。
1972年B.Y.Chen和K.Yano发表了论文《共形平坦空间的超曲面》。在该文中,他们利用“共表平坦空间中的共形平坦超曲面必定是拟脐点超曲面”的已有结果,讨论了常曲率空间中的共形平坦超曲面,由此引入了k-特殊共形平坦流形。该流形的曲率张量可表示为

式中a(≠const),β是二函数。
反之,每个k-特殊共形平坦流形必可等距嵌入常曲率空间作为超曲面而实现,这时(3)中α≠const的限制可取消。
这类流形与亚射影流形的关系是:集合{k-特殊共形平坦流形} {亚射影流形}。且它们都是介乎常曲率流形和共形平坦流形之间的两类流形。
{亚射影流形}。且它们都是介乎常曲率流形和共形平坦流形之间的两类流形。
自然要问,是否还存在另外这样的流形?如果存在,他们与上述两类流形有什么关系?对此,B.Y.Chen等人作出了部分回答。在1973年出版的《子流形的几何》中,B.Y.Chen提出了曲率张量K具有形式(1)的黎曼流形M,其度量g正定,且(1)中的向量场Z是伴随于M上的一个单位1-形式ω=ωidxi的向量场。
他指出这样的流形是共形平坦的,且具有以下3个性质:(i)伴随着垂直于向量场Z的二向量场X和Y的曲率算子 使Z消失,即K(X,Y,Z)=0。
使Z消失,即K(X,Y,Z)=0。
(ii)关于包含向量场Z的截面的截曲率是常数。(iii)关于和Z垂直的截面的截曲率是常数。后来K.Yano、C.S.Houh和B.Y.Chen又证明若n(>3)维黎曼流形M满足上述3个性质,则M的曲率张量必可写成形式(1)。
这表明拟常曲率流形的本质概念事实上是由B.Y.Chen首先提出的,尽管在提出时他没有采用“拟常曲率流形”这一术语。同时,从M为拟常曲率流形的上述充要条件(i),(ii)和(iii)可知,这类流形是特殊的共形平坦流形,但又不一定是常曲率流形。即拟常曲率流形确为介乎共形平坦流形和常曲率流形之间的一类流形。
最先明确提出“拟常曲率流形”这一概念的是V.Boju和M.Popescu。
《微分几何》杂志1978年发表了他们的论文《拟常曲率空间》。该文用纯几何的方法导出了这一概念,而简称其为QC空间。该空间M的一个几何特征是在其中存在向量场Z,使在每一点 ,都有Zp≠0,且所有截面σ∈(Zp,θ(p))的截面曲率彼此相等。这里
,都有Zp≠0,且所有截面σ∈(Zp,θ(p))的截面曲率彼此相等。这里 是σ在P点与Zp的交角。
是σ在P点与Zp的交角。
按此定义,在QC中选取正交单位活动标架场Z1,Z2,…,Zn=Z,V.Boju等两人求得了QC流形的曲率张量分量为:Kijji=H,Knjjn=N(i,j=1,…,n-1,且i≠j)其余为零。由此知曲率张量在此标架下可写成形式(1),其中 i,但这时ωn=1,ω1=…ωn-1=0。
i,但这时ωn=1,ω1=…ωn-1=0。
又因为表示形式是张量等式,故它在任何标架下都成立。也即(1)是QC的一个代数条件。
反之,这个代数条件被满足的正定度量的黎曼流形也一定是QC流形。因此(1)式就是QC流形的一个代数特征。从而,对于正定度量的黎曼流形,QC流形等价于拟常曲率流形。
当黎曼流形的度量不定时,对于拟常曲率流形的研究当首推白正国。
他在1982年发表的论文中证明:若一个n(≥4)维黎曼流形M可以等距嵌入于两个不同曲率K0和K1的常曲率空间,则M一定是共形平坦的,且得出了这样的M的一个代数特征。接着在1985年发表的另一论文中,白正国对这样的流形进行了详细的研究,并完全确定了其度量形式。进而,在1986年发表的《拟常曲率黎曼流形在常曲率空间中的等距嵌入》一文中,进一步明确证明前二文讨论的流形与拟常曲率流形是等价的。至此,才完成了“拟常曲率流形”这个概念的建立工作。
然而,这样建立的拟常曲率流形是否具有类似于QC流形的几何特征,并使得当流形的度量正定时,拓广的概念就是V.Boju等所引入概念的原有意义?关于此,在1987年发表的论文中,李中林作出了肯定的回答。
他证明曲率张量以形式(1)表征的黎曼流形M的一个几何特征是:其中存在一个向量场Z,使在每一点P∈M,所有截面σ∈(Zp,(P))的截面曲率彼此相等。
其中H(P)=e1<Z,X>2+e2<Z,Y>2,而<X,X>=e1,<Y,Y>=e2,<X,Y>=0。因此,称(1)式表征的黎曼流形为“拟常曲率流形”便有了实质的含义,且这一概念是对“QC流形”概念的拓广。
白正国把拟常曲率流形记为Q流形,并指出Q流形有值得注意的几何特性。事实上,这类流形除了上述已阐述的代数特征和几何特征外,还具有以下主要的特征性质:(1)拟常曲率流形等价于共形平坦的拟Einstein流形。
从而,它既是特殊的共形平坦流形,又是特殊的拟Einstein流形。
(2)黎曼流形M为拟常曲率流形的充要条件是M容有一族常数平均曲率的全脐点常曲率超曲面,而当超曲面为全测地时,M为拟Einstein的。
同时M的生成元就是超曲面的法向量。
现在可以把各类所涉流形组成的集合间的关系综述如下:{共形平坦流形} {拟常曲率流形}
{拟常曲率流形} {-阶共形平坦流形}
{-阶共形平坦流形}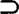 {k-特殊共形平坦流形}
{k-特殊共形平坦流形} {亚射影流形}
{亚射影流形} {常曲率流形}。
{常曲率流形}。
同时有:(1)拟常曲率流形为亚射影流形的充要条件是其生成元为测地线 。(2)拟常曲率流形为k-特殊共形平坦流形的充要条件是ωi∥▽i(nT-R)。
。(2)拟常曲率流形为k-特殊共形平坦流形的充要条件是ωi∥▽i(nT-R)。
这里“▽i”是协变微分算子。(3)若Q流形的数量曲率R为常数,则它必定是亚射影流形。(4)若Q流形的生成元是调和向量场,则它必为容有平行向量场的亚射影流形。当流形的度量正定时,(i)的结论曾为黄正中指明。
(5)Q流形的阶数为2的充要条件是R=2T≠0。由这些关系得知,Kagan意义的亚射影流形作为特殊的拟常曲率流形早在1930年就已被发现。
综上述,拟常曲率流形是较常曲率流形更广泛的一类流形,但又是特殊的共形平坦流形,具有值得注意的性质,因而引起国内外许多数学工作者的兴趣。
从70年代初发现开始,有关该流形的研究文献时有所见,限于篇幅,不能一一枚举。当前研究涉及的内容除了拟常曲率流表本身的性质,以及与已有流形的关系外,热点是关于子流形的讨论。一是把该流形作为常曲率空间的子流形的某些性质,另一则是讨论拟常曲率的子流形的一些性质,例如极小子流形、具有平行平均曲率向量场的子流形、不变子流形等的有关性质。
特别是探讨作为着名的Simons不等式的推广的不等式,以及相关的Pinching,问题,还有关于该流形上的特征值问题等。这一些问题的研讨均有待进一步展开。
所有这些问题的研究无疑对丰富微分几何的内容,保进微分几何的发展都是很有意义的。
。【参考文献】:
1 AdatiT. Tohoku Math,J 1951,3:l59~173
2 Chen BY. Tensor,N. S,1972,26:318~322
3 Chen B Y. Geometry of submanifolds. New York;Marcel Dekker Inc,1973,169~170
4 Boju V, Popescu M. Diff Geom, 1978,13:373~383
5 Bai Zhengguo Chin. Ann of Math, 1982,3(4) :471~482
6 Hwang Chengchung.数学研究与评论,1983,3(1)∶1~16
7 白正国.数学年刊,1986,7A(4)∶445~449
8 李中林.杭州大学学报(自然科学版),1987,14(2)∶158~168
9 Bai zhengguo.Chin Ann of Math,1988,9(1)∶32~37
10 李中林.杭州大学学报(自然科学版),1988,15(3);245~255
(杭州大学李中林教授撰;白正国审)