多项式时间度
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第1页(3405字)
由多项式时间界化归性所导出的等价类,是递归论及计算复杂性理论研究的重要内容,也是探讨P=?NP问题的一个重要途径。
在文献中,有各种各样的多项式时间化归性(简称p-化归性)被广泛讨论,其中的绝大多数是由对递归论中的化归性增加一个多项式时间界而导出的。然而,正如一般递归论中的情形一样,有两种化归性具有特别的重要性:第1种是由库克(S.A.Cook)在1971年首先引进的多项式时间图灵化归性(简称p-t化归性),这是最一般的多项式时间化归性;另一种是由卡珀(R.M.Karp)在1972年定义的多项式时间多一化归性(简称p-m化归性),这是一种限制极大的化归性,但对讨论大多数自然的问题来说已是足够的了。
p-化归性是作为证明某些问题之难解性的基本工具而引进的。
比如说,C是多项式时间可计算集类P的一个真扩张复杂性类,那么,我们只要证明某个问题是C-完全的或C-难的,那么,便可知该问题是非多项式时间可计算的。
与此相关,对NP-完全问题的研究被证明是十分有意义的。对p-化归性本身的结构以及由它们导出的度(简称p-度)结构的讨论也构成了一个十分有意义的研究内容。
实际上,这些讨论是结构复杂性理论的主要内容之一。
对p-度的讨论,其内容之一是讨论由p-度所组成的代数结构。这种讨论首先是由拉得纳(R.E.Ladner)在20世纪70年代开创的。他首先引进了延迟对角线方法,该方法成为这个领域中的一种基本技巧。
运用此法,他得到了许多有趣的结果(我们以p-r兼指p-t和p-m):递归集的p-r度之偏序结构〈RECp-r;≤〉是具最小元的上半格(即任何两个度都有上确界而多项式时间可计算集构成最小的度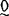 )并且是稠密的(即对
)并且是稠密的(即对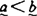 ,存在
,存在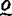 使
使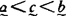 );每个非
);每个非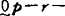 度可分裂成两个不可比较度的上确界;另外,存在极小对,即两个不可比较的度以
度可分裂成两个不可比较度的上确界;另外,存在极小对,即两个不可比较的度以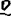 为下确度。
为下确度。
此后,上述结果得到了各种形式的加强,例如,麦尔洪(K,Mehlhorn)证明了每个有穷偏序可以嵌入到每个p-度区间中去;邱(P.Chew)、马希得(M.Machtey)以及朗特韦伯(L.H.Landweber)、利普顿(R.J.Lipton)、罗勃松(E.L.Robertson)等人在80年代初证明了对任何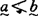 ,存在
,存在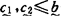 使
使 ,从而每个非
,从而每个非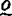 度都界有极小对。
度都界有极小对。
在此基础上,安勃思-斯皮思(K.Ambos-Spies)引进了更一般的对角线方法证明更强的可嵌入性结果,例如,他证明了每个可数分配格可以在保持最大最小元的条件下嵌入到任一p-度区间中去。这个结果可以推出上面所有结果。
上面这些结论强调了度结构的齐性和一致性,并且这些对全体度成立的结果限制到度区间上后仍成立。由此导出了齐性猜想:〈RECp-r;≤〉的任两个区间都同构。但是,安勃思-斯皮思通过分析浠疏集之下p-度的性质否定了这个猜想。并且他还证明了〈RECp-m;≤〉是分配的,而〈RECp-t;≤〉是非分配的,从而它们不同构。
进而,肖尔(R.A.Shore)和斯莱曼(T.A.Slaman)在1989年证明了任何有穷非分配格都可嵌入到(RECp-t;≤〉。
所有这些非齐性的结论都有一个共同的特点,即它们都需要延迟对角线之外的方法来证明,而要运用一种能行的有穷损伤方法来证明。
这是一种非常有力的方法,其核心是所谓加速技巧。这种技巧在下面提到的所有全域性质证明中都用到。但是,这种加速技巧有一个明显的缺点,它所构造的集合是非常复杂的,实际上都不是初等递归的。当然,这种高复杂性的特点有时也是有用的。
例如,安勃思-斯皮思利用这种技巧证明了关于递归集p-度的一个结论,而它对初等递归集又不成立。
关于多项式度讨论的另一个内容是关于p-度理论的讨论。
上述的非齐性结论是讨论多项式度一阶理论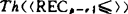 的可定义性问题的第一步。这种可定义性结果可用以把其它理论编码到p-度理论中去,从而得到不可判定性结论。这方面的第一个主要结论是希努达(J.Shinoda)和斯莱曼1990年证明的结果。他们证明了递归集的p-t度一阶理论
的可定义性问题的第一步。这种可定义性结果可用以把其它理论编码到p-度理论中去,从而得到不可判定性结论。这方面的第一个主要结论是希努达(J.Shinoda)和斯莱曼1990年证明的结果。他们证明了递归集的p-t度一阶理论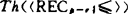 是不可判定的,并且它递归等价于一阶算术。
是不可判定的,并且它递归等价于一阶算术。
另一方面,肖尔和斯莱曼则在最近证明了〈RECp-t;≤〉的∑2-(或等价地,П2-)理论(即全体可在偏序语言L(≤)中用至多两个量词,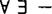 或
或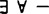 形的公式所能表示的定理集合)是可判的。
形的公式所能表示的定理集合)是可判的。
这两个结果的证明用到了p-t度结果的非可分配性,因此不能推到p-m度上去。
尽管安勃思-斯皮思在1985年就证明了理论Th(〈RECp-m;≤〉)具有非标准模型,只是最近安勃思-斯皮思和尼思(A.Nies)才证明了这个理论也是不可判定的。
然而,这个理论的度尚没被分类。到目前为止,其最好的可判定过程只能应用到∑1-理论。安勃思-斯皮思和勒曼(M.Lerman)目前正在研究把这个过程推广到∑2-理论。
在对p-度的讨论中,下列两个问题是这个领域中研究的热点。
(1)确定可以获得不可判定性结论的公式的逻辑复杂性,即找出恰好在哪一个量词水平上(对公式的前束范式而言),p-度的理论开始成为不可判定的。
由于目前使用的关于p-t和p-m度理论的不可判定性证明都用到了非常复杂的编码技巧,因此,只是在很高的量词水平上才得到了不可判定性结果。(2)确定可以获得不可判定结论的集合和度的计算复杂性,由于现有的不可判定性证明都用到了加速技巧,因而,只对一般递归集合或原始递归集合的p-度理论才适用。
但是尚不知初等递归集(或甚至是指数时间可计算的集合)的p-t度或pm度理论是否是可判定的。
。【参考文献】:1 Ladner RE. JACM, 1975.22: 1S5~171
2 Mehlhorn K. J. Comput System Sci, 1976,12:147~178
3 Chew P , Machtey M. J Comput System Sci, 1981,22: 53 ~59
4 Landweber L H, Lipton R J , Robertson E L. Theor Comput Sci, 1981,15:103~123
5 Ambos-Spies K. Tech Rep, 1985,206
6 Ambos-Spies K. Inform and Contral ,1985,65:63~84
7 Shore R A , Slaman T A. The p-t-degrees of the recursive sets: lattice embeddings, extensions of embeddins and the two quantifier theory,to appear
8 Shinoda J , Slaman T A. On the structure of the polynomial degrees of the recursive sets,to appear
9 Ambos-Spies K , Nies A. The theory of the polynomial many one degrees of recursive sets is undecidable,to appear
(南京大学郑锡忠博士撰)