太阳集和最佳逼近的特征

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第49页（2998字）

设E是赋范线性空间，，令

，

1961年，Garkavi对凸集M，给出刻划m₀∈P_Mx的Kolmogorov型特征定理：

M凸：，满足‖f‖=1，f(x－m₀)=‖x－m₀‖，Ref(m－m₀)≤0。

对于非凸集，上述Kolmogorov型特征定理能否成立?要使Kolmogorov型特征定理成立，M应满足怎样的充要条件?

为讨论最佳逼近的唯一性，1958年Efimov和Stechkin引入太阳集的概念如下：，m∈P_Mx_t，其中x_t=m+t(x－m)。1969年Brosowski证得：

定理B下列条件等价：(1)M是太阳集；(2)，m₀∈M有：，满足‖f‖=1，f(x－m₀)=‖x－m₀‖，Ref(m－m0)≤0。

关于太阳集，有下述结论：(1)1．M是太阳集等价于E，m₀∈M，，有m₀∈P_［m0，m］x，其中［m₀，m］=｛m_λ；m_λ=m₀+λ(m－m₀)，λ∈［0，1］｝；(2)M是太阳集，m₀是M对x的局部最佳逼近；(3)M是光滑空间E中的存在性太阳集凸；(4)M是严格凸空间E中的存在性太阳集是Chebyshev集；(5)设X紧，E为实C(X)，M是C(X)中太阳集等价于下列条件之一；(i)M对x的局部最佳逼近必为最佳逼近，(ii)M有闭符号性质：，m₁∈M，及满足(x)－m₀(x)｜＞0的闭集，则m₀属于｛m；m∈M，［m(x)－m₀(x)］［m₁(x)－m₀(x)］＞0，x∈A｝的闭包。

将最佳逼近的目标由单元x换成E中有界集F，即为最佳同时逼近问题，令

m₀∈P_M(F)称为M对F的最佳同时逼近。

对M是凸集的情形，1982年Freilich和Mclaughlin证得Kolmogorov型特征定理：

定理F－M M凸，，存在L∈extk满足。其中符号意义如下：

设，对E^*中闭单位球B^*，赋以σ(B^*，G)拓扑：，。

K取B^*的子集，满足：(1)K是σ(K，G)紧集；(2)，m∈M，有为K上函数，定义如下：

其中U(L)为L的邻域全体。

Freilich和Mclaughlin只对实空间E加以证明，复空间E的证明类似。

我们举出反例，指出定理F－M中L∈extK是错误的，应改正为L∈K．进一步，对于非凸集，我们于1987年得到

定理X－L 下列条件等价：

(1)M是同时太阳集：有界集F及m₀∈M，有，m₀∈P_M(F_t)，其中

F_t=｛f_i；f_i=m₀+t(f－m₀)，f∈F｝

(2)有界集F，，存在L∈K，满足，ReL(m－m₀)≤0。

再讨论M对｛f_i｝的P阶联合最佳逼近问题，设P≥1，数列｛λ_i｝满足λ_i≥0，，对任何满足的E中序列｛f_i｝，求m∈M，使最小。

在讨论中，我们固定｛λ_i｝，并令

并引入P阶联合太阳集的概念如下：，其中f_i，t=m₀+t(f_i－m₀)。

对P阶联合最佳逼近我们证得Kolmogorov型特征定理。

定理X P≥1，下列论断等价：

(1)M是E中P阶联合太阳集。

(2)满足，

其中Mf_i－m0=｛ψ；ψ∈E*‖ψ‖=1，ψ(f_i－m₀)=‖f_i－m₀‖｝

(3)，，，满足

其中ε(M_fi－m0)表示M_fi－m0的端点全体。

最后，讨论更一般的非线性优化问题，设E为线性拓扑空间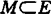，，ψ(x)为E上连续凸泛函，讨论优化问题：。记

并引入ψ太阳概念如下：记，若由m₀∈P_M(ψ)可推出m₀PC_m0(M)(ψ)，则称M为ψ太阳。

可证得：

定理X 设E为线性拓扑空间，ψ(x)是E上连续凸泛函，M，m₀∈M，则下列条件等价：

(1)M是ψ太阳

(2)，满足

Ref(m－m₀)≥0，其中

(3)，满足

Ref(m－m₀)≥0。

从特殊的优化：到一般非线性优化，最优解的特征的研究已有局部展开，对ψ(m)不凸、不光滑的情形，结果较少，今后可望得到进展。

ψ(m)从数值到向量值，从数值优化到多目标优化也是优化问题研究深化的重大一步，对非线性多目标优化问题的研究目前局限于有限维，对于一般情形，各种意义下的最优解的特征刻划是今后值得研究的课题。

。

【参考文献】：

1 EfimovN V.StechkinSB. D A N SSSR, 1958;118:17～19

2 Garkavi A L. Uspekhi Mat Nauk ,1961)16(4) :141～145

3 Brosowski B. Abstract spaces and approximation. ISNA 10 Birkhauser Verlag, 1969,140～159

4 Freilich J H, Mclaughlin H W. J A T, 1982,34:146～158

5 徐士英，等．数学学报，1987，30(4)∶528～535

(浙江师范大学徐士英教授撰)