拓扑分子格理论

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第85页（3457字）

按Bourbaki学派的观点，数学中有三大母结构，即代数结构、拓扑结构和序结构。

拓扑分子格理论是拓扑结构与序结构结合产生的一门新学科，它把近年来出现的Fuzzy拓扑学纳入拓扑格的理论框架之中，是点集拓扑学、Fuzzy拓扑学及L-fuzzy拓扑学的共同推广。

1965年，美国L．A．Zadeh提出Fuzzy集的概念。集X上一个Fuzzy子集A，实际上是从X到单位区间［0，1］的一个映射，这种映射的全体记作如果把X的通常子集B与其特征函数等同看待的话，那么B实际上是从X到｛0，1｝的一个映射，这种映射的全体是｛0，1｝^x。因为，所以Fuzzy子集的概念是通常子集概念的推广。1968年C．L．Chang提出Fuzzy拓扑空间的概念，他称［0，1］^x的一个子族δ为X上的Fuzzy拓扑，如果0，1∈δ且δ对有限交与任意并运算封闭，这里0，1分别表示X上最小与最大的映射，而交与并分别指映射取下确界与上确界的运算，称序对()为Fuzzy拓扑空间。有了这个Fuzzy拓扑δ，一系列的基本概念似乎就可仿效点集拓扑学中的相应概念而得出。

如，称δ中的Fuzzy集为开集，称包含于Fuzzy集A中的最大Fuzzy开集为A的核，记作A⁰；若H′=1－H∈δ，则称H为闭集；称包含A的最小闭集为A的闭包，记作A^－；称()为紧空间，若X的每个开覆盖U(即且supU=1)都有有限子覆盖；等等。其实，由于｛0，1｝^x与［0，1］^x有许多相似之处(如，De Morgan对偶律都成立，联系两个空面的基本映射也有许多共同的性质等)，点集拓扑学中的那些立足于这些共同基础的命题自然也就在Fuzzy拓扑空间中成立而无需再进行任何证明。

正因如此，C．L．Chang曾乐观地说：“一般拓扑学中的许多基本概念可以容易地推广到Fuzzy拓扑空间中去”。然而，人们很快就发现，由于比一般拓扑空间多了一个序结构，Fuzzy拓扑学要比一般拓扑学远为复杂，比如上面提到的用有限覆盖的方法在Fuzzy拓扑空间中定义紧性很快就被发现是完全失败的。

事实上，［0，1］^x与｛0，1｝^x虽然有若干共同性质，但差别毕竟是巨大的。如，排中律不成立(即，与A∨A′=1不再成立)，择一原则不成立(即，从推不出存在i₀使xλ∈A_i0)等。

这些都是重大的原则性差异，以致使点集拓扑学中以点的邻域系为基本工具的传统方法在Fuzzy拓扑学无法适用。这一情况迫使国外的学者回避Fuzzy点的观点。1975年，B．Hutton首先引入了Fuzzy正规空间的概念，而涉及到Fuzzy点的正则空间等概念则是以后才引入的。先引入正规性的理由，用Hutton的话来说，是因为“正规性是可单纯由开集和闭集(即，不涉及点)的语言加以定义的。”如果说这种做法在一开始时还不很自觉的话，那么M．A．Erceg则在他的一篇文章中公开宣称：“在探讨Fuzzy集理论时，我们发现在普通集理论中的点并不是如所想像的那么重要了”。实际上，从1975年以来，无点派确实作了不少工作。

如，Hutton在极小族、Fuzzy单位区间和Fuzzy一致结构等方面的工作至今在Fuzzy拓扑学中仍占有重要地位，但无点派的兴起毕竟是由于有点化研究没有出路而带来的结果。在此情况下，蒲保明与刘应明打破传统的邻域方法，引入具有重要意义的“重域”的概念，为有点派的研究开辟了道路。

从格论的角度来看，无论是在上展开的点集拓扑还是在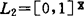上展开的Fuzzy拓扑，都是某种格L上的拓扑，从而也都可以纳入拓扑格理论之中。G．Nöbeling的书对此早有论述，只是其框架过于广泛以致于所得出的具体结论过于贫乏。特别是由于缺少点的概念及其相应的邻近结构理论，从而像仿紧性等这样重要的局部性质、像嵌入理论等这样基本的研究课题等都无法讨论。因此，我们自然想到去构造一种新的拓扑理论，使它一方面具有相当的广泛性，至少能把点集拓扑学与Fuzzy拓扑学二者都作为特殊情况而包含在内，同时又保留点集拓扑学的点式风格和丰茂的研究成果。

正是基于这种考虑，王国俊于1979年提出《拓扑分子格(I)》的理论。这样一种格L，其中含有充分多的类似于点的无素，叫做分子，它是点集拓扑学中点的概念以及Fuzzy拓扑学中Fuzzy点的概念的抽象化。它一方面起着基本单位的作用，任何元素都可表示为分子之并，另一方面它又不是最小的和不可分的。

这也正是我们称之为分子而不称其为原子的原因。

对于分子，提出了它的远域系概念，这是对点集拓扑学中邻域概念以及Fuzzy拓扑学中重域概念进念变革与抽象，基于以排斥远来刻划近的思想所提出的概念。利用远域这一工具，成功地建立起了分子的Moore-Smith收敛理论。

同时，在拓扑分子格范畴中还提出了一种新的态射一序同态，它是从通常映射与Zadeh型函数的众多性质中抓住其正向保并与逆向保对合这两条性质并加以抽象化而得出的。事实证明正是那两条性质起着关键作用，整个理论的展开也表明把序同态作为拓扑分子格范畴中的态射是恰当的。

这样，分子、远域与序同态就成了拓扑分子格理论的3个支柱。

1983年，王国俊又提出了《广义拓扑分子格》理论，对分子的概念作了大幅度的推广，而远域与序同态这两个概念则保持不变。不久就发现Fuzzy格L是满足这一广义理论的，从而该理论已经把L-fuzzy拓扑学作为特例而包含在内了。此后，又注意到逆序对合对应的存在对拓扑分子格理论的展开并不起什么重要作用，王国俊于1985年又提出了《完全分配格上的点式拓扑理论》，这里已不再要求格L上具有逆序对合对应存在，L可以是不对称的。

这时基于闭元概念的远域工具照样适用，但重域工具已无法应用。同时更清楚地看到，就邻近结构而言，远域结构具有最广泛的适用性。

与此对应的一个事实是：闭的概念比开的概念更为重要。再者，由于一个分子的远域构成一个理想，因而在广泛的框架之下理想的收敛理论就要取代与邻域方法相配套的渗透的收敛理论，至于序同态，由于逆序对合对应已不复存在，把逆向保对合的要求改为逆向保并，就产生了广义序同态理论。

至此，拓扑分子格理论已形成了初步完整的理论体系。点集拓扑学中的一些着名的定理与理论，如，Kuratowaski14集定理、杨忠道定理、樊畿定理和拟一致结构理论等也已成功地推广到了拓扑分子格理论之中。

拓扑分子格理论今后的研究热点是：(1)高次分离性的研究，包括正则、完全正则与正规分离性等。(2)与闭相对偶的开的概念的研究。

(3)紧性与仿紧性理论的研究。(4)一致结构与度量化问题的研究。预计在以上各问题的研究中后两个问题将会于近年内取得进展。

。

【参考文献】：

1 Nobeling G．Grundlagen der analytischen topologie，Springer -Verlarg，1954

2 Zadeh L A．Information and Control，1965，8：338～353

3 Chang C L．J Math Anal，Appl，1968，24：191～201

4 王国俊．科学通报，1983，28，1089～1091

5 蒲保明，刘应明，J Math Anal，Appl，1980，76：571～599

6 王国俊．中国科学(A辑)，1983，12：1063～1072

7 王国俊．陕西师大学报(自然科学版)，1985，1～2

8 樊太和．科学通报，1986，31：244～249

9 刘应明．Fuzzy Sets and System，1987，21：43～51

(陕西师范大学博士生导师王国俊撰)