洛伦茨曲线

出处：按学科分类—经济 经济科学出版社《消费经济学大辞典》第366页（1166字）

用来表示收入或财富分配不平均程度的曲线。由奥地利统计学家洛伦茨(Max Otto Lorenz)提出。是一种图示手段(如图)，由一个正方形、正方形的对角线以及至少一条连结对角线两端的曲线所组成。正方形的横坐标代表人口数的累积百分比，从0%到100%，纵坐标代表收入(或财富)的累积百分比，从0%到100%。连接两对角的直线OY为绝对平均曲线，该线上任何一点表示：总人口中每一定百分比的人口所拥有的收入量在总收入中也占有相同的百分比，该社会的收入分配是绝对平均的。OPY线是分配绝对不平均线，表示全社会的收入都归一人所有，其余人的收入为零。实际收入分配曲线介于绝对平均线和绝对不平均线之间，在此曲线上(OAY)除了起点和终点以外，任何一点到两轴的距离不相等。实际收入分配曲线与绝对平均曲线越接近，社会收入分配越接近平均；反之，这两条曲线差距越大，社会收入分配越不公平。洛伦茨曲线的方程为：

式中，y＞0代表收入水平；P表示人口累积百分比(收入小于y的累计人口占总人口的百分数)；I表示收入累积百分数(收入小于y的所有人的累计收入占总收入百分数)；ρ(u)表示收入的密度函数；μ是收入的期望值或社会的平均收入，即：

(1)式表示收入小于y的累计人口分布函数；

(2)式表示收入小于y的所有人的总收入的分布函数。

洛伦茨曲线的特征有：(1)P(0)=0，I(0)=0，即0%的人口拥有0%的收入；P(+∞)=1，I(+∞)=1，即100%的人口拥有100%的收入。(2)其斜率等于收入水平与平均收入之比，且大于零，即：

表示曲线是从原点向右上方上升。(3)曲线是向下凸的，即：

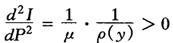
洛伦茨曲线的明显形式可由方程(1)和(2)导出：

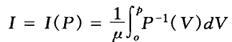
式中P^－1(V)是P(y)的反函数。洛伦茨曲线同计量单位无关，因此用该曲线可对不同地区、不同国家的收入分配情况进行比较；检验政府税收和财政收支的收入分配效应；检验财富分配的不平均程度。如果改变P(y)和I(y)的意义，还可以用来衡量市场结构的垄断程度或物品管理(如ABC法)。洛伦茨曲线的一个缺陷就是绝对平均线并非每个社会都想达到，对不同文化的社会进行比较时，并不能总是准确地反映它们之间的福利差别。

〖参〗基尼系数