完全信息条件下的消费者选择

出处：按学科分类—经济 经济科学出版社《消费经济学大辞典》第57页（1337字）

又称完全信息条件下的消费者行为(Consumer Behavior under Perfect Information)，是在完全信息和消费者收入、商品价格及其效用函数等初始条件既定的前提下，消费者如何选择满足约束条件的最佳商品组合的行为理论。

在完全信息条件下，消费者对各有关变量在选择前和选择后的结果都是确定的。如收入、价格甚至商品质量等信息都是确定的。

实际上，在这种信息环境里，有关商品的所有信息都反映到价格里了，消费者均衡可以通过市场机制得到实现。在完全信息环境里，消费者均衡问题实际上可以归结为技术性的优化问题，可用优化理论解决。

下面先以两种商品的情形说明之。两种商品、只有预算约束的优化问题的数学模型可表述为：

maxU=U(x₁，x₂) (1)

s．t．p₁x₁+p₂x₂=m (2)

其中U代表效用函数，m是收入，x₁和x₂是商品1和商品2的消费量或需求量，p₁和p₂分别是商品1和商品2的价格。

构造拉格朗日函数：

L(x₁，x₂，λ)=U(x₁，x₂)+λ(m－p₁x₁－p₂x₂) (3)

其中λ是拉格朗日乘子。效用极大化的必要条件(或一阶条件)是：

其中，

，

由(4)和(5)得：

U₁／p₁=U₂／p₂=λ (7)

这表示最后支付一个货币单位购买商品1所得的效用等于购买商品2所获得的效用。

由(7)还可得：

U₁／U₂=MRS₁₂=p₁／p₂ (8)

这表明当消费者均衡时，商品1替代商品2的边际替代率等于其价格之比p₁／p₂。由(8)可知，最佳商品组合是预算线与无差异曲线族中的某条无差异曲线相切的切点E所代表的商品组合(如图所示)。

(7)和(8)就是效用极大化的必要条件(或一阶条件)。

效用极大化的充分条件(二阶条件)是加边海塞(Hessian)行列式大于0，对于两种商品的情形，即：

其中，D是加边海塞三阶行列式，

根据一阶条件和效用函数严格准凹性假设能够保证二阶条件(9)成立。

这是因为由(4)和(5)可将D写成：

上述过程可推广到n种商品的情形，其最优化问题的数学模型可表述为：

其中，是需求量列向量，是价格行向量。拉格朗日函数是：

一阶条件是：

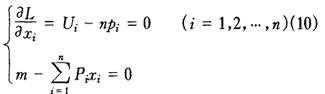
条件(10)也可写成：

U₁／P₁=U₂／P₂=…=U_n／P_n=λ

二阶条件是在最佳商品组合

(x₁^*，x₂^*，…，x_n^*)

处各阶加边海塞行列式的符号是正负交错的：

效用函数严格准凹性和一阶条件能够保证上述二阶条件成立。

〖参〗信息不对称条件下的消费者选择