高阶系统的单位阶跃响应

出处：按学科分类—工业技术 北京理工大学出版社《新编液压工程手册上册》第141页（1287字）

(1)表达式

高阶系统闭环传递函数的一般形式为

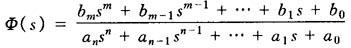
对上式进行因式分解，得

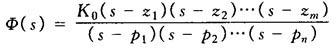
式中 K₀=b_m／a_n；

z_i(i=1，2，…，m)——系统闭环传递函数的零点；

p_j(j=1，2，…，n)——系统闭环传递函数的极点。

假定系统所有零点、极点都互不相同。n个极点中有q个实数极点，r对共轭复数极点(q+2r=n)。零点中只有实数零点。则系统单位阶跃响应的拉氏变换为

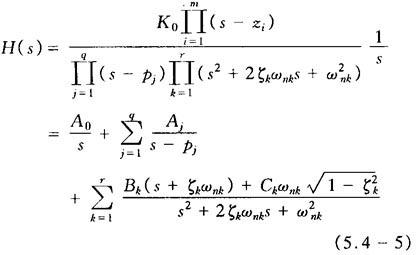
式中A₀、A_j、B_k、C_k都是在作部分分式时所确定的常数。

对式(5．4－5)取拉氏反变换，可得系统的单位阶跃响应表达式如下：

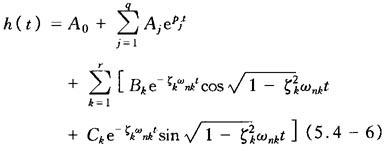
(2)闭环系统零、极点对单位阶跃响应的影响

A．极点至虚轴的相对距离对过渡过程的影响

对于稳定的系统，闭环系统极点具有负实部，其暂态分量随时间t增大而衰减，其中远离虚轴的极点所对应的暂态分量衰减很快，在整个系统到达稳态之前早已消逝，而那些离虚轴较近的极点所对应的暂态分量衰减很慢，在整个过渡过程中始终起作用。所以，过渡过程的主要特征取决于靠近虚轴的极点。经验证明，某些极点至虚轴的距离大于最靠近虚轴的极点至虚轴的距离5倍时，其对应的暂态分量对过渡过程的影响可以忽略。

B．零点对过渡过程的影响

一般来说，零点的存在使系统的过渡过程加快，上升时间缩短而超调量增大，零点离虚轴越近，这种影响越强。如果有一对零极点靠得很近，它们之间的距离小于该极点至虚轴距离的十分之一时，称此对零极点为偶极子，它们产生的总影响可忽略不计。

(3)主导极点和等效二阶系统

一个高阶系统，如果存在靠近虚轴的一个实数极点或一对共轭复数极点，并且在其附近又无零点，其它极点或因远离虚轴或为偶极子而可忽略，则这个或这对极点称为此高阶系统的闭环主导极点，它决定系统过渡过程的主要特征。由于欠阻尼情况的二阶系统有较好的过渡过程品质，所以在实际系统中常取主导极点为共轭复数。具有一对共轭复数主导极点的高阶系统可以用其主导极点所对应的二阶系统来近似，此二阶系统称为原高阶系统的等效二阶系统，并可通过对等效二阶系统的分析来估计原高阶系统的过渡过程性能指标。