电路的暂态分析方法
书籍:现代综合机械设计手册下
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册下》第2638页(1040字)

电路由一种稳定状态转换到另一种稳定状态的中间过程,称为暂态过程。产生暂态过程的充要条件是,电路在换路前后储能元件中的能量要发生变化。产生暂态过程的实质是能量的转换不能跃变。
分析电路暂态过程的依据是元件的伏安关系、克希荷夫定律和换路定律。采用经典法计算电路暂态过程的步骤如下:
①列出电路换路后待求量的微分方程;
②求待求量的稳态分量(即非齐次微分方程的特解);
③求待求量的暂态分量(即齐次微分方程的通解,也称补函数);
④确定积分常数,求待求量的完全响应(也即微分方程的完全解)。
根据微分方程理论,待求量的完全响应为:
完全响应f(t)=稳态分量f。+暂态分量ft
三要素法:在恒定输入作用下,一阶线性电路暂态过程的完全响应f(t),可由三要素快速公式求得,即
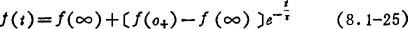
式中 f(∞)为电压或电流的稳态值;f(o+)为电压或电流的初始值;τ为电路的时间常数(s)。
时间常数体现电路的固有性质,它与外加电源无关,同一电路只有一个时间常数。它等于电路的暂态分量衰减到初始值的36.8%所需的时间。在电阻电容和电阻电感电路中,时间常数分别为
式中 R0为电路换路后由储能元件两端看进去的等效电阻。
仅仅由电路的初始储能产生的响应,称为零输入响应,用f′(t)表示,其表达式为
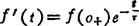
仅仅由电路中的电源或信号源作用产生的响应,称为零状态响应,以f″(t)表示,其表达式为
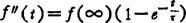
完全响应=零输入响应+零状态响应。其表达式为
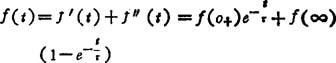
上一篇:RLC串联电路的暂态过程
下一篇:现代综合机械设计手册下目录