预处理
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册下》第2871页(4663字)
在插补运算之前,一般都应进行数据的预处理,以便把最直接、最方便形式的数据提供给插补运算,提高系统的实时处理能力。数据的预处理包括确定坐标平面、刀具半径补偿的计算、坐标位移量的计算(绝对值和增量值),及速度处理等。
4.3.1 刀具半径补偿
一般零件的程序是按其外形尺寸编制的,可数控机床的走刀控制却以刀具中心为基准,因此对于铣刀存在刀具半径补偿,对于车刀除刀具半径补偿外,还有刀长补偿。
完成刀具半径补偿功能,需用G40、G41和G42。G40用于取消刀补,G41、G42用于建立刀补。沿刀具前进方向看,G41表示刀具在工件的左边,G42表示刀具在工件的右边。若上一程序段是G40状态,本程序段是G41或G42状态,则该程序段处于刀具补偿建立方式。刀具补偿建立程序段必须是直线程序段。如果上一程序段是G41或G42状态,本程序段仍是G41或G42状态,则该程序段处于刀具补偿方式。若上一个程序段是G41或G42状态,本程序段是G40状态,则该程序段处于刀具补偿取消方式。
在一般情况下,程序段之间的交接有直线与直线、直线与圆弧和圆弧与圆弧三种情况。当直线与直线、直线与圆弧、圆弧与圆弧不相切时,就会造成刀具中心轨迹线的不连续或干涉,如图8.5-50所示。通常需用尖角过渡的方法予以解决。常用的尖角过渡方法有圆弧过渡法和直线过渡法。
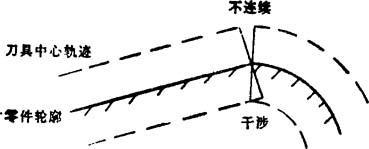
图8.5-50 尖角造成的不连续或干涉
圆弧过渡法就是在程序中增加一段圆弧过渡程序。尖角过渡圆弧的圆心以及起点和终点很容易由工件轮廓求出,圆弧的半径即为刀具半径。这种方法只适用于凸的轮廓尖角。采用圆弧过渡法,应考虑过渡圆弧的跨象限。此外,圆弧过渡法不可避免的在拐角处有一停顿时间,从而使尖角处的加工工艺性变差,尖角往往被加工成小圆角。
采用直线过渡法时,对于凸的轮廓尖角采用延长求交点作为程序段终点,而对于凹的轮廓尖角则采用缩短求交点作为程序段终点,如图8.5-51所示。图中b点为程序段终点。应该指出,铣床无法加工出工件的凹尖角,在工件尖角处将留有以铣刀半径为半径的圆弧轮廓。因此,对于内表面的尖角,编程时应说明允许的最大铣刀半径。
在具有刀具补偿功能的计算机数控(微机数控)系统中,为确定第N程序段的工作方式,并对其编程轨迹进行必要修正,除知道第N程序段的信息外,还必须知道第N+1程序段的信息。因此,仅有工作寄存器不能满足需要,还需设置缓冲寄存器,有的系统还另外设置刀补缓冲器,如图8.5-52所示。图中,BS为缓冲寄存器,CS为刀补缓冲寄存器,AS为工作寄存器,OS为输出寄存器。第N段程序先被读入BS,在BS中算得的第N段编程轨迹送至CS暂存、再将第N+1段程序读入BS,并算出其编程轨迹。接着,对第N、N+1段编程轨迹的连接方式进行判别,根据判别结果对CS中的第N段编程轨迹进行修正。而后,将CS中的内容送AS,BS中的内容送CS。然后由CPU将AS中的内容送OS进行插补运算,驱动伺服系统。在第N段程序执行过程中,CPU利用插补间隙将第N+2段程序读入BS…。可见,这种系统在刀补工作状态时,系统内总是同时存三个程序段的信息,OS可以连续得到刀补修正后的程序内容进行插补输出。
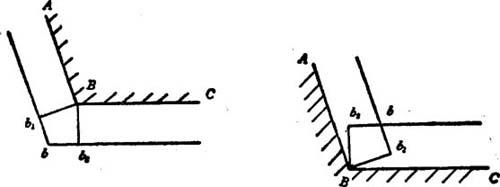
图8.5-51 直线尖角过渡的程序段终点
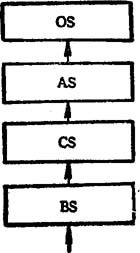
图8.5-52 CNC系统的寄存器设置
对于刀具半径补偿,最基本的有直线→直线、直线→圆弧、圆弧→圆弧和圆弧→直线四种情况。图8.5-53所示为直线→直线,其中BC为要加工的数据段,根据已知的该数据段的编程增量xBC、yBC,计算刀具中心轨迹bc的增量xbc、ybc。这样,当系统控制刀具从b点运动到c点时,刀具便自动加工出轮廓RC。由图可知:
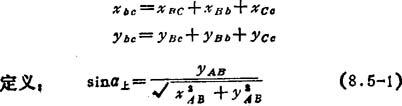
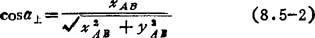
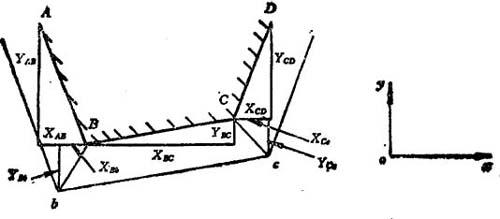
图8.5-53 直线→直线刀具半径补偿原理
因为xAB、yAB有正有负,所以sina上、cosα上也有正有负。同理,可列出sinα本、cosα本、sinα下、cosα下。若设r刀为刀具半径,则根据三角函数关系可以导出
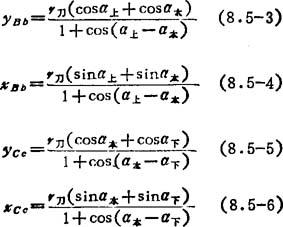
计算出以上各值,也就得到xbc、ybc。应该指出,xBb、yBb在对AB段进行刀具半径补偿时已经算出,在对BC段进行刀具补偿时只需译出CD段信息,计算出xCc、ycc即可。
下段为圆弧的情况如图8.5-54所示。这种情况包括直线→圆和圆→圆。对sinα下、cosα下作如下定义:
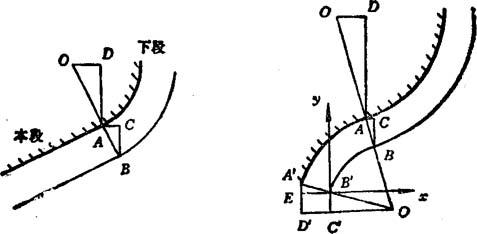
图8.5-54 下段为圆弧情况的刀具半径补偿原理
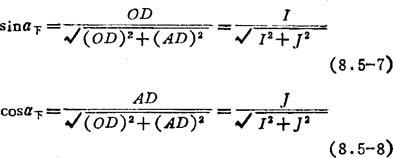
其中I、J为圆弧段的圆心相对圆弧起点的坐标。图中,三角形OAD中的OD和AD分别为编程中的I和J,三角形ABC中的BC和AC分别为y偏和x偏。两个三角形相似,因此下面的计算公式成立:
x偏=y刀·sinα下;y偏=γ刀Cosα下 (8.5-9)
本段为圆弧时,还需计算本段刀具中心的I、J。如图所示,OD′为本段的I值,A′D′为本段的J值,这在编程时已给出。B′E为上段和本段之间的X偏,A′E为上段和本段之间的y偏,这在对上一段进行刀具半径补偿时已算出。于是由图可得
I=本段程编I值+上段和本段的X偏 (8.5-10)
J=本段程编J值+上段和本段的y偏 (8.5-11)
圆→直线如图8.5-55所示。对于本段
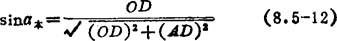
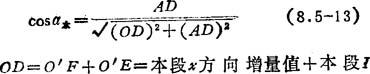
AD=AF+FD=本段y方向增量值+本段J值因为三角形OAD与三角形ABC相似,AB为刀具半径V刀,BC、AC分别为本段与下段之间的x偏和y偏,所以可得
x偏=r刀sinα本; y偏=v刀Cosα本 (8.5-14)
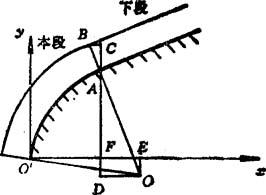
图8.5-55 圆→直线刀具半径补偿原理
本段刀具中心的I值和J值的计算与圆→圆的情况相似。
图8.5-56所示为刀具半径补偿的原理框图。
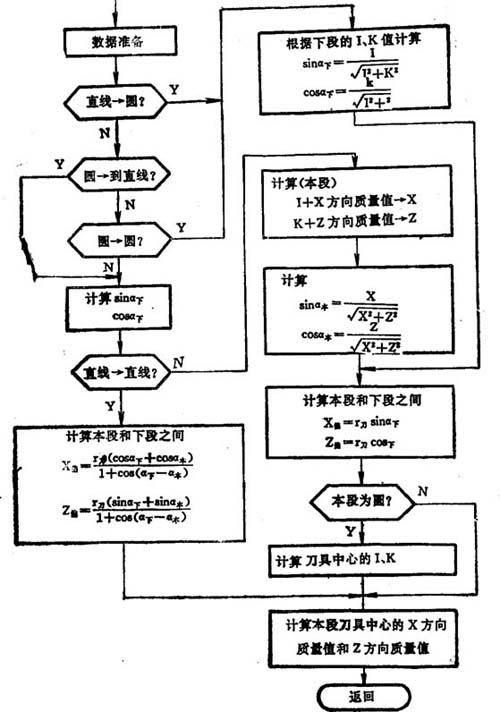
图8.5-56 刀具半径补偿原理框图
4.3.2 速度计算
对于开环系统,坐标轴的运动速度由输出的进给脉冲频率决定。速度的计算,就是根据程编的进给速度F值确定该频率值。而对于闭环或半闭环系统,则是基于时间分割的思想,根据程编的进给速度,将轮廓曲线分割成采样周期的进给量,即轮廓步长。其速度计算的内容是.直线插补时,计算出各坐标采样周期的步长;圆弧插补时,计算出步长分配系数(或称角步距)。
开环系统的速度计算:开环系统的进给速度F(mm/min)与脉冲发送频率f(脉冲/s)及脉冲当量δ(mm/脉冲)之间有如下关系:
F=f·δ·60(mm/min) (8.5-15)根据进给速度F计算出脉冲发送频率f,就可使坐标轴按要求的速度进给。计算机数控系统获得要求频率的方法有:1.用实时时钟中断法,即按照计算得到的f值预置适当的实时时钟,以产生频率为f的定时中断;2.用软件模拟数字积分器,即将计算得到的f值作为被积函数,在一定容量的累加器中按一定频率累加,有进位则输出脉冲;3.采用软件延时,即根据计算得到的f值算出输出脉冲的时间间隔,减去插补运算及脉冲输出时间,即是软件延时时间。计算机数控系统控制步进电机的方法是:1.用输出脉冲作为内部插补迭代的控制信号,每来一个脉冲,调用一次插补子程序;2.用输出脉冲作为外部控制信号,即用来控制插补结果的输出。
闭环、半闭环系统的速度计算:通常采用的是数据采样插补的方法。直线插补时,速度计算是为插补程序提供各坐标轴在一个周期中的运动步长,如图8.5-57所示.采用直接指定法设定速度时,
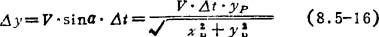
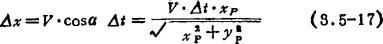

图8.5-57 直线插补
式中 V为程编速度;Δt为采样周期;xP(yP)为x方向(y方向)程编增量。
采用进给速率数(FRN)设定速度时,

其中L为程编段的轮廓尺寸,在直线和圆弧的情况下分别为,
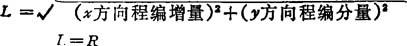
步长公式如下:
Δy=FRN·Δt·(y方向程编分量)=λd·(y方向程编分量) (8.5-19)
Δx=FRN·Δt·(x方向程编分量)=λd·(x方向程编分量) (8.5-20)
其中,λd=V·Δt/L,称为速度系数。
圆弧插补的情况如图8.5-58所示。坐标轴在一个采样周期内的步长按下式计算:
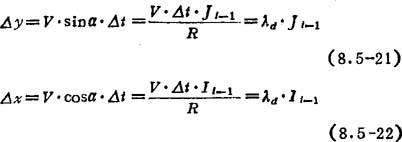
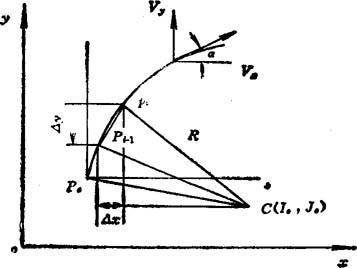
图8.5-58 圆弧插补
其中,Ii-1和Ji-1为圆心相对于第0-1点的坐标;λd=V·Δt/R,称为步长分配系数,为常量;λd与圆弧上一点的I、J值的乘积可以确定到下一插补点各坐标轴的进给步长。由此可见,圆弧插补速度计算,就是计算步长分配系数λd,为插补提供速度信息。