操作手的雅可比矩阵

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2088页（3388字）

(Jacobian)

操作手运动学的正问题和逆问题，从正反二方面研究了关节状态矢量与末端装置的位置与方位之间的关系。在运动控制中，尚需确定关节的无穷小运动在末端装置位置与方位无穷小变化之间的关系。在无穷小关节运动与无穷小末端装置运动之间存在一线性关系。这一关系可用雅可比矩阵定义。若设末端装置的微小移动和微小转动为d和δ，则

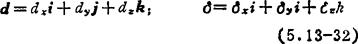
把这二个矢量合并为一个微运动矢量的列阵，以dD表示，则

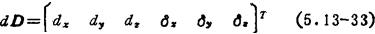
设操作手有6个关节，6个关节变量组合在一起成为一个六维关节变量矢量

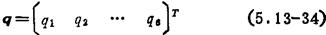
运动副微变化矢量为

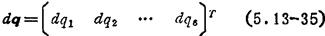
操作手雅可比矩阵为J，则

dD=Jdq (5．13-36)

J是一个6×6矩阵。两边都除以无限小时间增量dt，得

D=J q 5．13-37)

其中 D=〔v(t)Ω(t)〕^T (5．13-38)v(t)和Ω(t)是末端装置相对于基座坐标的线速度和角速度。于是(5．13-37)式成为

其中J_j(q)是雅可比矩阵第j列的6×1矢量，可以表示为

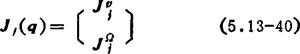
于是末端装置的线速度和角速度分别为

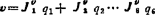(5．13－41)

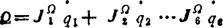
从上式看出，由第j个关节广义速度q_j产生的末端装置的线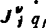速度为，角速度为。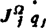

图5．13-37是一个机器人的结构草图。从图中看出，如果第j个是转动关节，关节的转动使第j杆直至末端装置都以同一角速度转动，当第j关节轴上的单位矢量为z_j－1，则j运动副转动的角速度为ω_j=z_j－1θ_j，j关节的转动使末端装置产生线速度。设j－1p₀为j－1杆系原点至末端装置夹持中心的位置矢量，由j关节转动对末端装置线速度v的奉献为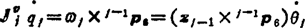 (5．13-42)

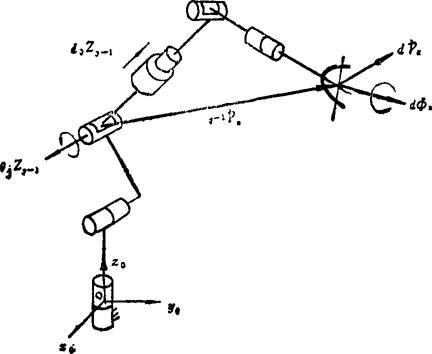
图5．13-37 关节广义速度对末端装置的影响

j关节转动对末端装置角速度Ω的奉献为

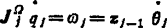
(5．13-43)

总起来，如果j关节为转动关节，则

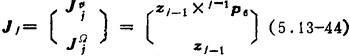
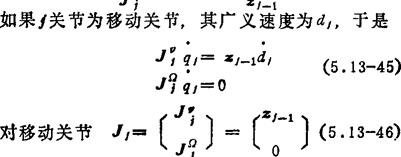
对于PUMA和Stanfovd机器人，其雅可比矩阵分别为

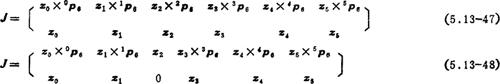
以矢量表示雅可比矩阵的元素，形式简单，概念清晰。但^j－1p₅为〔T－⁰A₁¹A₂…^j－2A_j－1〕的第四列的计算工作量很大。为此，可以把各矢量元素向n、a和a轴投影表示。对于转动关节：

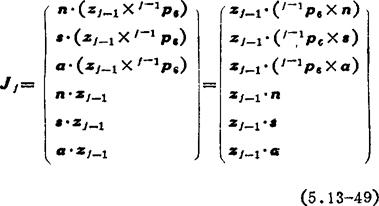
并且在x_j－1、y_j－1和z_j－1坐标系中计算上式中各矢量。于是^j－1z_j－1=〔001〕^T，设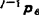=〔^j－1p_x^j－1p_y^j－1p_z〕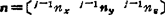，，依次类推。于是

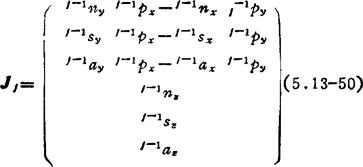
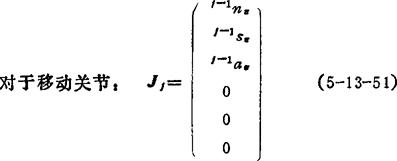
计算步骤是：先计算⁵T₆=⁵A₆，⁴T₆=⁴A₅⁵A₆，…^j－1T₆=^j－1A_j…⁵A₅，而

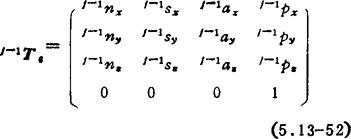
在以上计算中，雅可比矩阵各列在不同坐标系中投影计算所得各元素为标量。与计算所选用坐标无关，因此不失其普遍性。但是计算工作量也较大。一般在计算末端装置的速度时，速度参考点取在夹持中心。为了简化计算，设想末端装置扩大到包含腕上一点W，并且把瞬时与W重合的点(虚的)作为计算速度的参考点来计算J。各矢量向以W为原点的坐标系投影表示，且取x_4、y₄和z₄。为与前面各式一致，设x₄=n⁴、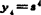、z₄=a⁴。则

对于转动关节

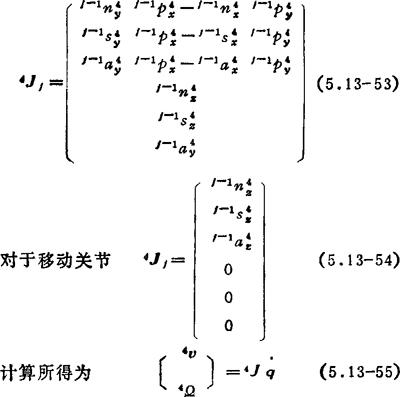
由以下公式计算末端装置的线速度v和角速度Ω：

6v_x=⁴n·〔(⁴Ω×⁴p)+⁴v〕

6v_y=⁴8·〔(⁴Ω×⁴p)+⁴v〕

6v_z=⁴a·〔(⁴Ω×⁴p)+⁴v〕 (5．13－56)

4Ω_x=⁴n·⁴Ω

6Ω_y=⁴z·⁴Ω

6Ω_z=⁴a·⁴Ω

其中⁴n、⁴3、⁴a和⁴p是⁴T₆中的列阵，即

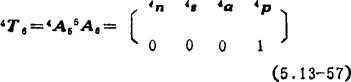
计算步骤如下：

5T₄=⁴A_；^－1 计算⁴J的第六列。

4T₄=J 计算⁴J的第五列。

3T₄=³A₄ 计算⁴J的第四列。

2T₄=²A₃³A₄ 计算⁴J的第三列。

1T₄=¹A₂²A₃³A₄ 计算⁴J的第二列。

0T₄=⁰A₁¹A2²A₃³A₄ 计算⁴J的第一列。

以上矩阵的计算较为简单，因此计算雅可比矩阵元素的工作量可大为减少。现以图5．13-38所示简化PUMA机器人为例，说明雅可比矩阵的求法。各杆系的变换矩阵为2

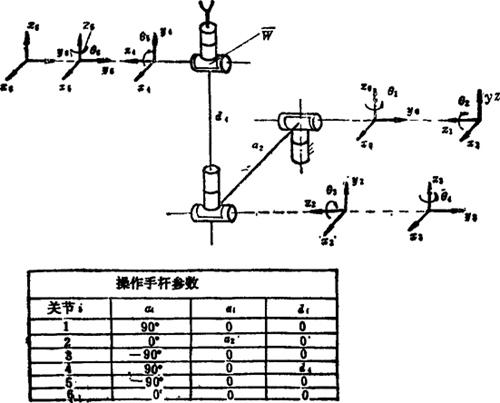
图5．13-38 简化PUMA机器人

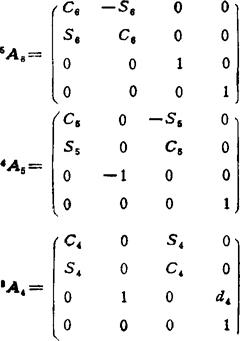
由于关节2和3的轴是平行的，可用¹A₃=¹A₂²A₃代替¹A₃和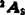，故需要计算的矩阵为：

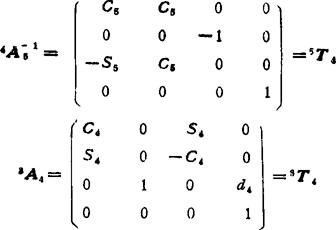
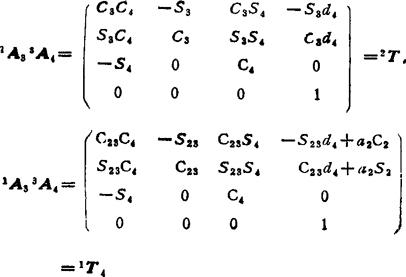
从以上各式中即可得到式(5．13-53)和(5．13-54)的各变量。因为

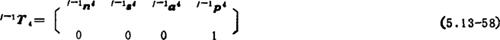
由(5．13-53)式计算操作手雅可比矩阵各列，得

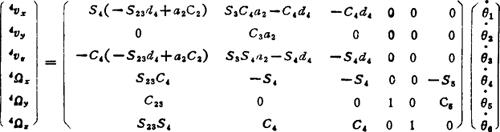
雅可比矩阵元素中有重复项，上式等价于

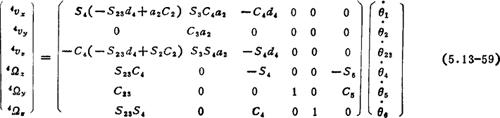
式中θ₂₃=θ₂+θ₃。由(5．13-57)式计算⁴n、⁴a⁴a和⁴p，得

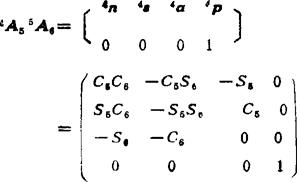
由(5．13-56)式得

6v_y=－C₅S₆⁴v₂－S₅S₆⁴v_y－C₆⁴v₂

6v₂=-S₅4v_x+C₅4v_y

6Ω_x=C₅C₆⁴Ω₂+S₅C₆⁴Ω_y-S₆⁴Ω₂

6Ω_y=－C₅S6^＇Ω₂－S₅S₆4Ω_y－C₆4Ω₂

6Ω₂=－S₅⁴Ω_x+C₅4Ω_y

计算⁴J只需11次乘法运算和3次加法运算；求⁴v和⁴Ω需要16次乘法运算和12次加法运算；求⁶v和⁶Ω需要20次乘法运算和10次加法运算。总数分别为47次和25次。