傅立叶变换
书籍:现代综合机械设计手册上
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第30页(1171字)
11.2.1 傅立叶积分的几种形式
设函数f(x)在无穷区间(-∞,+∞)上绝对可积,定义f(x)的傅立叶积分为
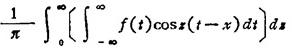
若f(x)的傅立叶积分满足收敛的条件,则傅立叶积分有以下几种形式:
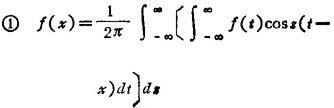

③若f(x)是偶函数,则
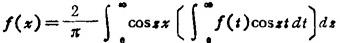
④若f(x)是奇函数,则
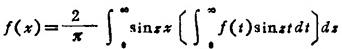
11.2.2 傅立叶变换
定义:设函数f(x)满足
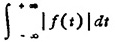
存在:f(x)在(-∞,∞)上满足狄利克莱条件即f(x)只有有限个极值点,只有有限个第一类间断点,则存在
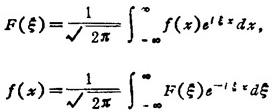
称F(ξ)为f(x)的傅立叶变换,第二式称为傅立叶变换的反演公式。
傅立叶变换的性质:设f(x),g(x)的傅立叶变换分别是F(ξ),G(ξ),则
线性 af(x)+bg(x)的傅立叶变换是aF(ξ)+bG(ξ)。
卷积 f(x)*g(x)=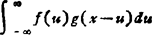 的 傅立叶变换是F(ξ)·G(ξ)。
的 傅立叶变换是F(ξ)·G(ξ)。
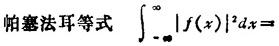
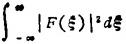
翻转 f(-x)的傅立叶变换是F(-ξ)。
共轭 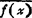 的傅立叶变换是
的傅立叶变换是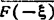 。
。
时移(延迟) f(x-x0)的傅立叶变换是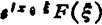 。
。
频移(调频) F(ξ-ξ0)是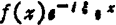 的傅立叶变换(ξ0是常数)。
的傅立叶变换(ξ0是常数)。
11.2.3 傅立叶变换表
见表1.1-16。
表1.1-16 傅立叶变换表

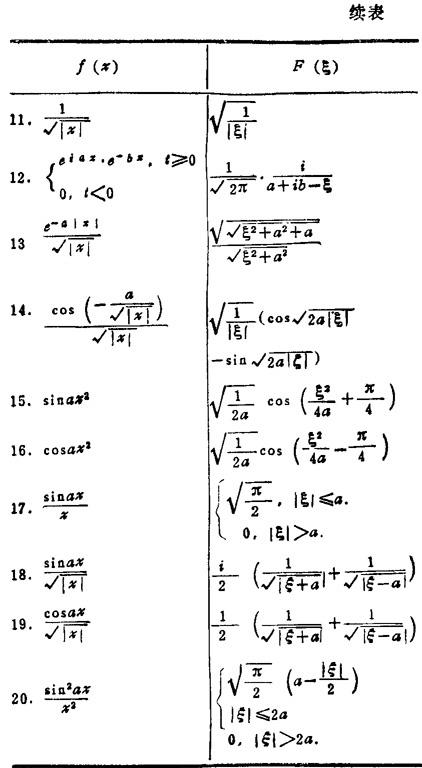
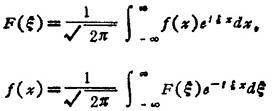
上一篇:拉普拉斯变换
下一篇:现代综合机械设计手册上目录