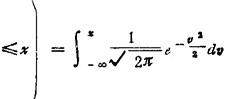概率论

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第37页（3542字）

14．1．1 概率的基本性质

①0≤P(A)≤1，P(A)=1－P(A)，A为任何事件。

②P(Ω)=1，P(Φ)=0，Ω、Φ分别表示必然事件和不可能事件。

③若A、B互斥，则P(AUB)=P(A)+P(B)否则，P(AUB)=P(A)+P(B)－P(A∩B)

④若A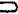B，则P(A)≥P(B)，且P(A)－P(B)=P(A＼B)

⑤若A₁，A₂，…，A_n是两两互斥的事件完备组。则P(A₁UA₂U…UA_n)==P(A₁)+P(A₂)+…十P(A_n)=114．1．2概率的计算公式

①条件概率与乘法公式。在事件B发生的条件下，事件A发生的概率称为A在B已发生的条件下的条件概率，记作P(A|B)，当P(B)＞0时，规定

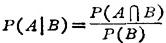
乘法公式为

P(A∩B)=P(B)P(A丨B)=P(A)·P(B|A)

P(A₁A₂…A_n)=P(A₁)P(A₂|A₁)P(A₃|A₁A₂)

…P(A_n|A₁A₂…A_n－1)

P(A₁A₂…A_n－1)＞0

②独立性公式。如果事件A与B满足P(B|A)=P(B)则称事件B关于事件A是独立的。

A与B相互独立的充要条件是

P(A∩B)=P(A)P(B)

如果事件A₁、A₂，…，A_n中任意m个(2≤m≤n)都满足关系式

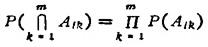
则称A₁，A₂，…A_n是总起来独立的，简称相互独立。

③全概率公式。如果事件组B₁，B₂，…满足

B_j∩B_j=Φ(i≠j)，P(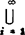B_i)=1，P(B_i)＞0，(i=1，2，…)

则对于任一事件A有

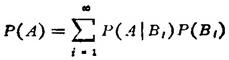
对于有限个事件公式同样成立。

④贝叶斯公式。如果事件组B₁、B₂，…满足

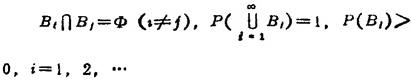
则对于任一事件A(P(A)＞0)有

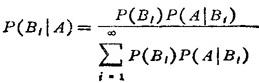
对于有限个事件组，公式同样成立。

⑤伯努利公式。设一次试验中某事件A出现的概率为ρ，则n次重复试验中事件A出现k次的概率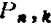为

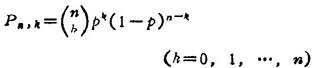
当n和k都很大时，有近似公式

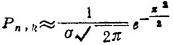
式中

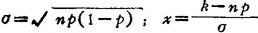
⑥泊松公式。(5)中当n充分大，且ρ很小时，有近似公式

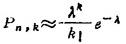
式中 λ=nρ。

14．1．3 随机变量的数字特征

(1)数字期望(平均值)

①离散随机变量的数字期望。设随机变量ξ取可数个值x₁，其相应的概率为p_x，则称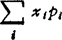为ξ的数字期望，记作Eξ(或Mξ)，即

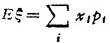
②连续随机变量的数字期望。设随机变量ξ的概率密度为户(x)，若积分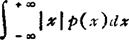收敛，则称之为ξ的数字期望，记作Eξ(或Mξ)，即

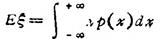
(2)方差

若随机变量(ξ－Eξ)²的数字期望存在，则称E(ξ－Eξ)²为随机变量ξ的方差，记作Dξ，即

Dξ=E(ξ－Eξ)²

离散随机变量的方差

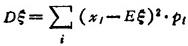
连续随机变量的方差

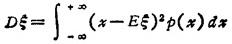
均方差(或标准差) σ=

(3)契比雪夫不等式

对任何具有有限方差的随机变量ξ，都有

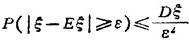
式中 ε是任一正数。

(4)关于数字期望与方差的运算

①Dξ=E(ξ－Eξ)²=Eξ²－(Eξ)²

②设c为常数，则Ec=c，Dc=0，E(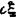)=cEξ，D(cξ)=c²Dξ

③E(ξ+η)=Eξ+Eη

④设ξ、η互相独立，则E(ξη)=Eξ·Eη，D(ξ+η)=Dξ+Dη

⑤E(ξη)=Eξ·Eη+cov(ξ，η)

式中

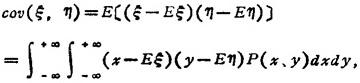
cov(ξ、η)称为随机变量系(ξ，η)的相关矩。若ξ，η独立，cov(ξ，η)=0。

⑥D(ξ，η)=Dξ+Dη+2cov(ξ+η)

14．1．4 几种常用的概率分布

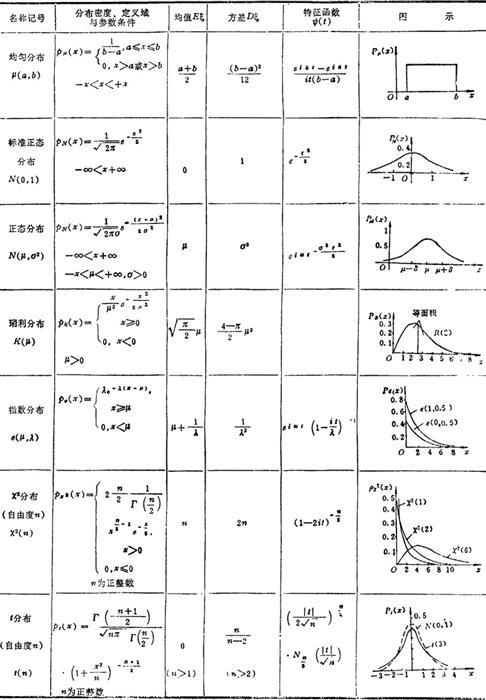
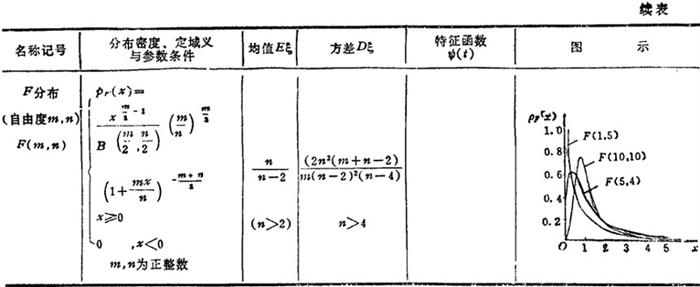
常用离散型分布和连续型分布分别见表1．1－18和1．1－19。

表1．1－18 常用离散型分布

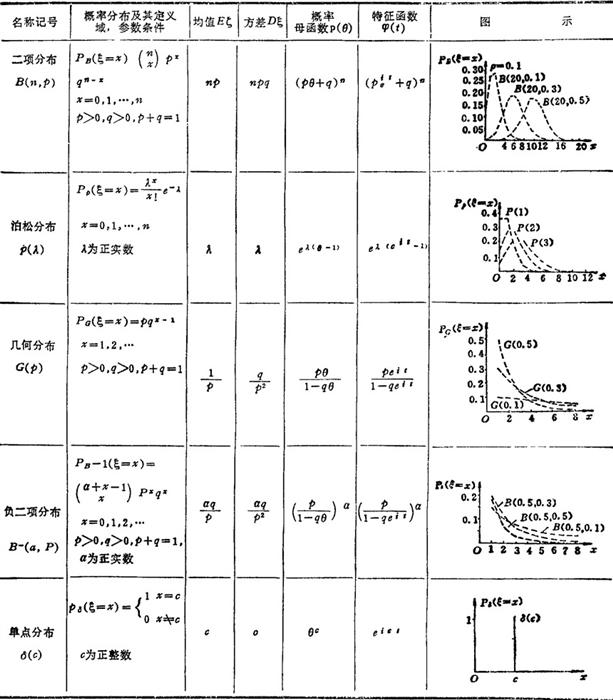
表1．1－19 常用连续型分布

14．1．5 大数法则与中心极限定理

(1)大数法则

伯努利定理：随机事件A在n次独立试验中的频率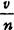依概率收敛于事件A的概率ρ，即对任意e＞0，

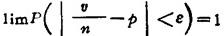
互相独立的随机变量ξ₁，ξ₂，…，如果(i)存在均值和方差，记作Eξ_k=μ，Dξ_k=σ²(k=1，2，…)；或者(ii)具有相同分布，且有有限均值Eξ_k=μ，那么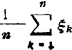依概率收敛于随机变量的均值Eξ_k=μ，即对任意ε＞0，

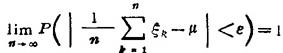
如果互相独立具有相同分布的随机变量ξ₁，ξ₂，…的均值和方差都存在，记Eξ_k=μ，Dξ_k=σ²

(k=1，2，…)，那么

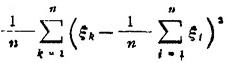
依概率收敛于随机变量的方差Dξ_k=σ²，即对任意ε＞0，

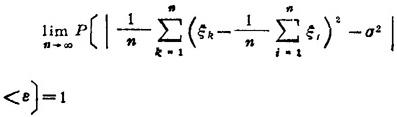
(2)中心极限定理

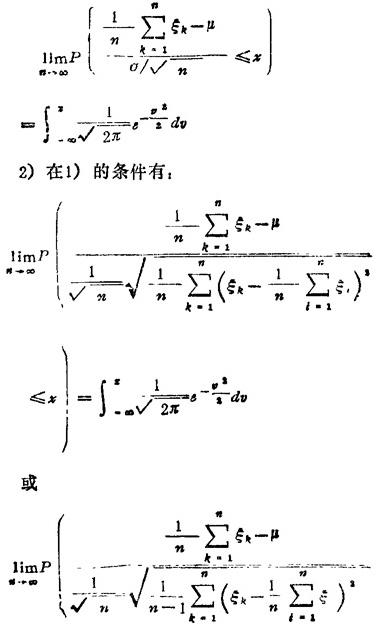
1)如果互相独立具有相同分布的随机变量ξ₁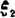，，…的均值和方差都存在，记Eξ_k=μ，Dξ_k=σ2(k=1，2，…)，那么随机变量

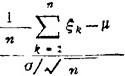
渐近地遵从标准正态分布N(0，1)，即