当前位置：首页 > 经典书库 > 现代综合机械设计手册上

数理统计

书籍：现代综合机械设计手册上

出处：按学科分类—工业技术北京出版社《现代综合机械设计手册上》第41页（4604字）

14．2．1 总体参数的估计

(1)样本特征数与总体数字特征对照表

见表1．1－20。

表1．1－20 样本特征数与总体数字特征对照表

(2)总体参数的点估计

①矩估计法。用样本矩作为相应的总体ξ的矩估计量：

②最大似然法。似然函数

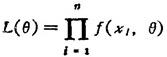
式中 f(xi，θ)是随机变量xi的概率分布；θ为有待估计的参数。

由方程=0或=0解出的θ是x₁，x₂，…x_n的函数，使L(θ)达到最大值的θ(x₁，x₂，…x_n)记作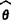(x₁，x₂，…，x_n)，称为总体参数θ的最大似然估计量。若参数不止一个，可用偏导数代替导数。

(3)样本的频率分布

频率分布较完整地反映实验数据的变化规律。

注：当n较大时，取s²=建立频率分布的步骤是(设样本为x₁，x₂，…，x_n)：

①找出最大值和最小值，求得极差R==max｛x1｝－min｛x₁｝；

②根据样本大小分组，通常大样本分成10～20组，小样本分成5～6组，再根据组数k和极差R决定组距c，如果按等距分组，则c≈；

③确定分点(常取比原数据精度高一位)；

④数出各组的频数v₁；

⑤计算频率；

⑥作直方图(分点为横坐标，频率与组距之比为纵坐标)：

⑦如果变量是连续的，则描出光滑曲线，近似地代替总体的分布。

(4)总体参数的区间估计

总体参数的区间估计列于表1．1－21。假设总体遵从正态分布N(μ，σ²)。对于预先给定的置信度a，可用一个样本x₁，x₂，…x_n的均值x和标准差s来估计总体的μ和σ2的置信区间，也可以用两个样本｛x₁₁，x₁₂，…，x_1n｝和｛x₂₁，x₂₂，x_2n｝的，和s₁，a₂来估计两个总体均值差μ₁－μ₂的置信区间。

表1．1－21 总体参数的区间估计表

14．2．2 统计检验

(1)参数假设检验

正态总体参数的统计检验方法如表1．1－22所列。对于大样本，不管总体遵从什么分布，根据中心极限定理，可以认为样本均值x渐近遵从正态分布，因此利用“μ检验法”对总体参数进行统计检验。

表1．1－22 正态总体参数的统计检验表

(2)非参数假设检验(要求大样本)

对确定的分布函数的x2检验方法如下：

①假设H₀：ξ～F(x)(已知F(x)的分布类型及参数)。

②根据样本的范围把实轴分成k个不相交区间S₁=(c₁，c₂)；Si=(c₁，c_l+1)(i=2，3，…，k)，使样本在每个子区间S_i中出现的个数u₁≥5。计算理论频率：v₁=F(c₁₊₁)－F(c_i)=P(c_₁≤ξ＜c₁₊₁)。

③选取统计量

式中的n为样本实验或观测次数。

④确定给定置信度a下的否定域u≥u_a，u_a由确定。

⑤计算统计量的观察值μ，可作出如下判断：当μ≥μ_a时，拒绝原假设H₀；当μ＜μ_a时，接受原假设H₀。

对于分布函数的类型已知，而参数未知的x2检验方法如下：

①假设H₀：ξ～F(x)，已知F(x)的类型，但有l个未知参数λ₁，λ₂，…，λ₁。

②用最大似然确定l个参数的估计量，…。

③划分区间S_i，确定v_i，u_i。

④选取统计量

式中的n为样本实验或观测次数。

⑤确定给定置信度a下的否定域u乡u_a，u_a由确定。

⑥计算统计量的观察值u，并获得如下结论：当u≥ua时，拒绝原假设H₀；当u＜u_a时，接受原

表中a为给定量信度，为样本均值，s为样本标准差假设H₀。

14．2．3 方差分析

(1)单因素方差分析

问题提法：考虑一个因素A的不同水平对所考察对象的影响。对A的k个不同水平A_i(其分布～N(μ_i，)，i=1，2，…，k)进行试验，得到试验数据｛x_if｝(i=1，2，…，k；j=1，2，…n_k)。假定σ₁=σ₂=…=σ_k，检验各Ai的试验结果的平均值有无显着差异。

检验步骤：

①假设H₀：μ₁=μ₂=…=μk。

②选取统计量并明确其分布

式中

③确定给定置信度a下的否定域F≥F_a，F由(k－1，n－k)dv=a确定

④作统计量

⑤按表1．1－23获得统计推断。

表1．1－23 单因素方差分析表

(2)双因素方差分析

考虑两个因素A和B的影响。A分成l个等级A₁，A₂．…，A₁；B为分成m个等级B₁，B₂，…，B_m。在双因素A_i×B_j条件下(即每次试验都让A_i与B_j作l·m种配合)作n次试验，得lmn个数据(k=1，2，…，n)；i=1，2，…，l；j=1，2，…，m)。假定｛｝的分布服从N(μ_if，σ²)，检验A的作用或B的作用或A×B的作用分别对试验结果有无显着影响。其检验步骤如下：