刚体上力系的简化
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第56页(2155字)
1.2.1 基本力系的简化
(1)汇交力系的简化
各力作用线相交于一点的力系称为汇交力系。汇交力系总可简化(合成)为合力。合力的大小和方向等于汇交力系主矢的大小和方向,合力的作用线过此汇交力系的汇交点。由合矢量的投影定理知,合力R在直角坐标轴上的投影等于各力在相应轴上投影的代数和,即

式中 Rx、Ry、Rz、Xi、Yi、Zi分别为合力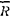 及
及
第i个力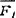 在x、y、z各轴上的投影。
在x、y、z各轴上的投影。
(2)力偶系的简化
力偶系能且只能简化为合力偶,不可能简化为一不等于零的合力。合力偶的力偶矩矢等于各力偶矩矢的矢量和,即

式中 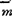 、
、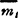 分别为合力偶与第i个力偶的力偶矩矢。
分别为合力偶与第i个力偶的力偶矩矢。
1.2.2 任意力系的简化
任意力系可简化为作用于任一确定点(称为简化中心)的一个力和一个力偶。该力的力矢等于原力系的主矢,该力偶的力偶矩等于原力系对简化中心的主矩。即任意力系(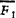 ,
,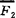 ……
……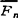 n)向简化中心Ο简化所得到的力矢
n)向简化中心Ο简化所得到的力矢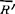 和力偶矩矢分别为:
和力偶矩矢分别为:
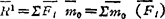
根据原力系的主矢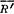 和主矩
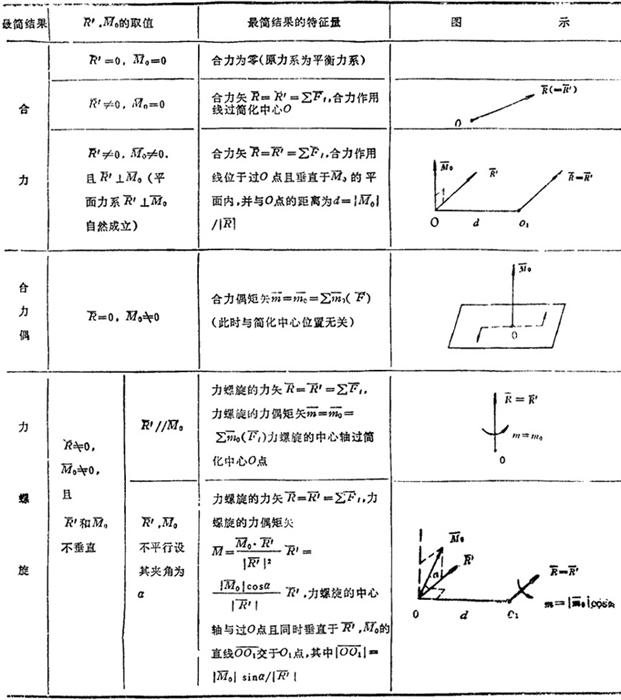
和主矩 0的不同结果,向简化点简化所得到力和力偶还可继续简化为下属三种情况之一:合力;合力偶,或力螺旋(1)。具体情况见表1.2-1。
0的不同结果,向简化点简化所得到力和力偶还可继续简化为下属三种情况之一:合力;合力偶,或力螺旋(1)。具体情况见表1.2-1。
表1.2-1 力系简化的三种最简结果
1.2.3 力系简化的实例
(1)平行力系的中心和重心
同向平行力系总可合成(简化)为一合力,而且当各力的作用点和大小保持不变的条件下,无论怎样改变各力的共同方向,其合力的作用线都将过空间唯一的确定点C。此点C称为该平行力系的中心。物体各微元所受地球引力可近似认为是一同向平行力系,此平行力系的中心就称为物体的重心。
重心的计算公式见表1.2-2;简单均质形体的重心(形心)位置见表1.2-3。
表1.2-2 重心位置计算公式
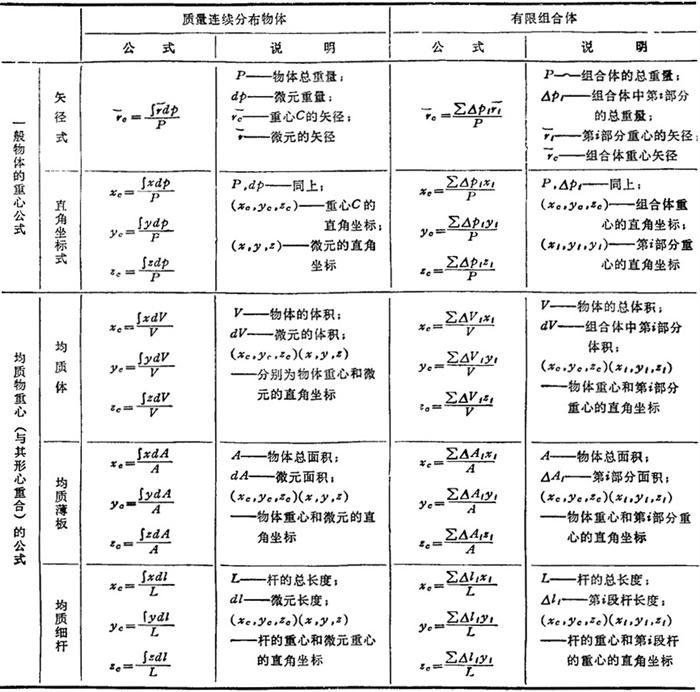
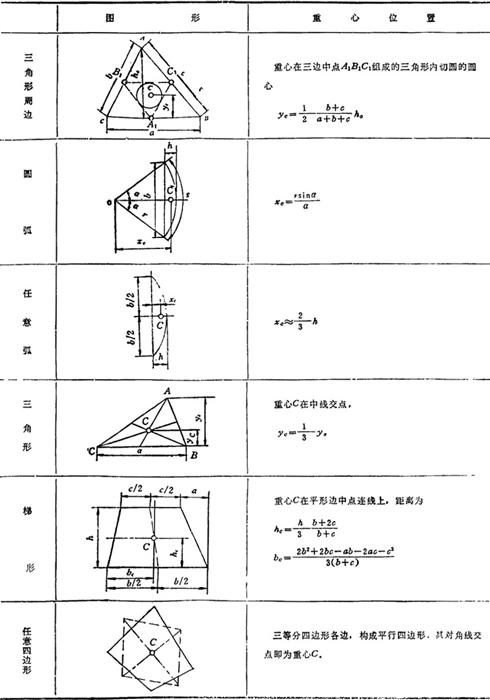
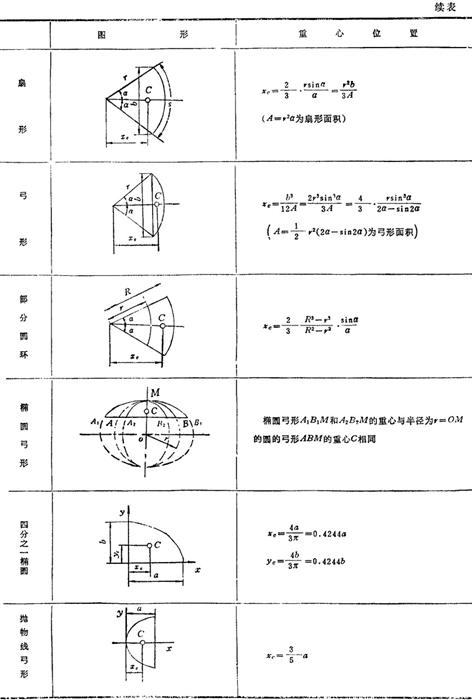
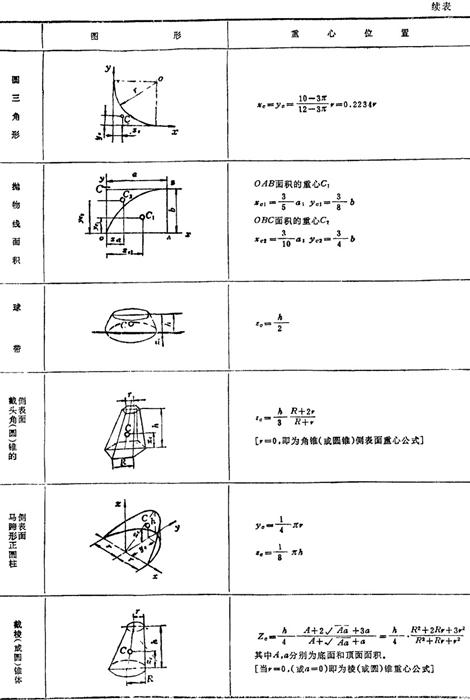
表1.2-3 均质形体的重心位置
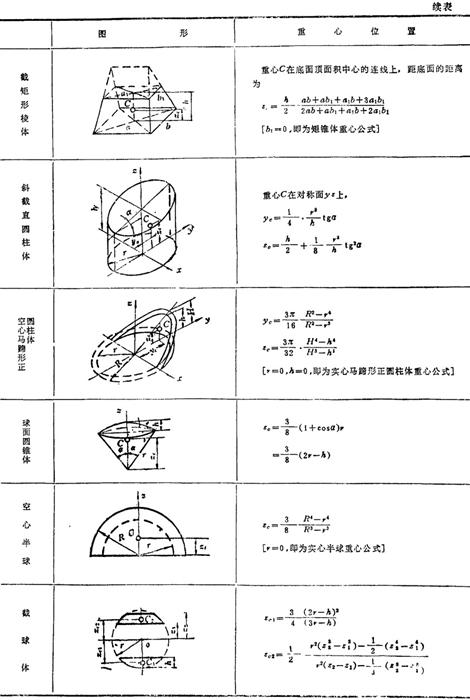
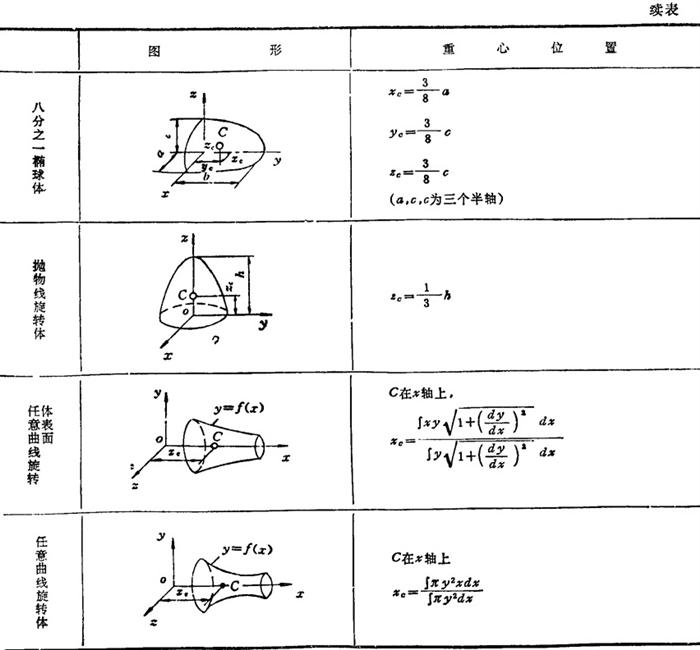
(2)其它力系简化实例
例1.2-1 如图1.2-6所示,在边长为α的正方形平板上作用着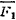 ,
,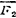 ,
,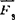 三力,各力的大小均为P。试求此三力的最简简化结果。
三力,各力的大小均为P。试求此三力的最简简化结果。
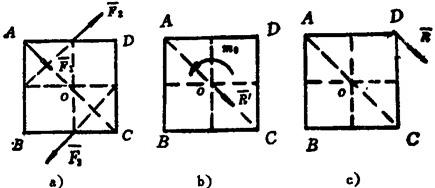
图1.2-6 力系简化实例一
解:计算力系主矢
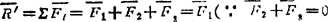 )选取Ο为矩心,计算力系主矩
)选取Ο为矩心,计算力系主矩
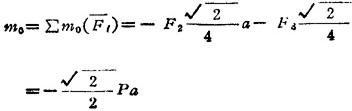
可见力系可简化为作用于O点的一个力和一个力偶(图1.2-6b)。
由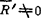 ,
,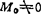 ,可知力系还可进一步简化为一合力R。由
,可知力系还可进一步简化为一合力R。由
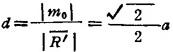
可知合力作用线过正方形顶点D(图1.2-6c)。其合力矢为
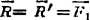
例1.2-2边长为a的正方体上作用二等值力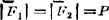 ,其作用线位置和方向如图1.2-7(a)所示。试求此二力的最简简化结果。
,其作用线位置和方向如图1.2-7(a)所示。试求此二力的最简简化结果。
解:建立如图坐标系Oxyz。计算力系的主矢
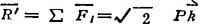
计算力系对O点的主矩
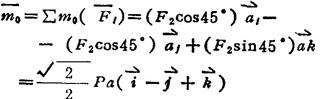
显而易见,由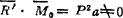 知,
知,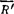 和
和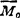 不垂直,故力系最简结果为一力螺旋。
不垂直,故力系最简结果为一力螺旋。
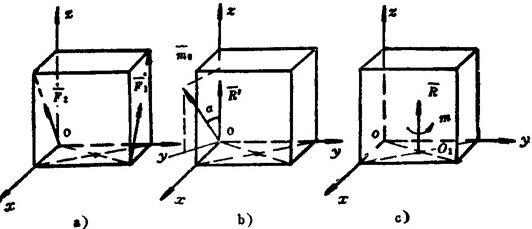
图1.2-7 力系简化实例二
由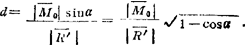 其中
其中
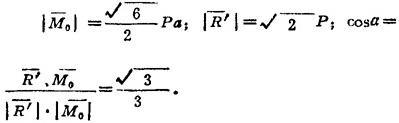
故代入上式化简可得
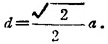
可知力螺旋的中心轴过底面中点O1。力螺旋的力矢和力偶矩矢分别为(图1.2-7(c)):