质量几何

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第81页（1690字）

3．1．1 质心

质心是质量中心的简称，它是质点系质量分布的平均位置，其基本公式见表1．2－17。

表1．2－17 质心的基本计算公式

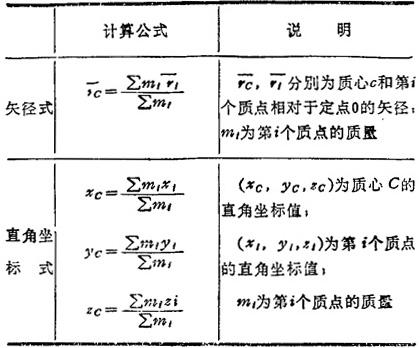
在工程中，质点系的质心和它的重心重合。有关计算质心位置的方法可参见1．2．3。

3．1．2 刚体的转动惯量和惯性积

刚体对轴L的转动惯量：刚体绕轴L转动时惯性的度量，也称惯性矩。其值为

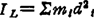(1．2－38)

式中m₁为刚体中第i个质点的质量；d1为该质点至轴L的距离。

若刚体质量连续分布，则刚体对L轴的转动惯量为

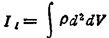
式中 ρ为体积元dV的质量密度；d为该积分元至轴L的距离。

惯性积：刚体上每个质点的质量m_，与其两个直角坐标的乘积之总和，称为刚体的惯性积，也称离心转动惯量，即

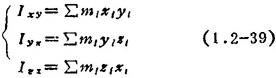
对于质量连续分布的刚体，它的三个惯性积分别为

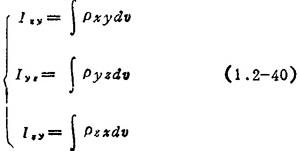
式中 ρ为体积元dv处的质量密度；(x，y，z)为该体积元的直角坐标值。

刚体对过坐标原点O处任一轴之转动惯量可由以下公式计算：

IL=I_xa²+I_yβ²+I_．γ²－2I_xyαβ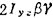－－2I_zxγα (1．2－41)

式中 I_x，I_y，I_z为刚体对坐标轴的转动惯量；l_xy，I_yz，I_zx为刚体对坐标轴的惯性积；α，β，r为轴L与各坐标轴的方向余弦。

刚体对L轴的回转半径定义为：

式中 m为刚体的总质量。

转动惯量的平移轴公式为：

I_L=I_CL+ml² (1．2－43)

式中 I_L为刚体对任意轴L的转动惯量；I_CL为刚体对过质心C且与L轴平行的轴CL的转动惯量；l为L与CL的距离；m为刚体的质量。

匀质刚体的转动惯量见表1．2－18。

表1．2－18 均质物体的转动惯量

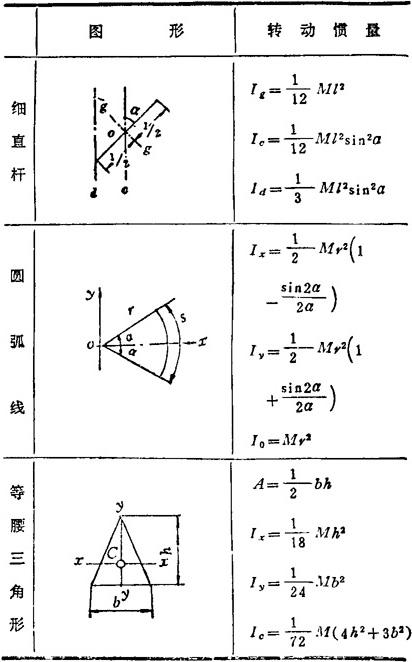
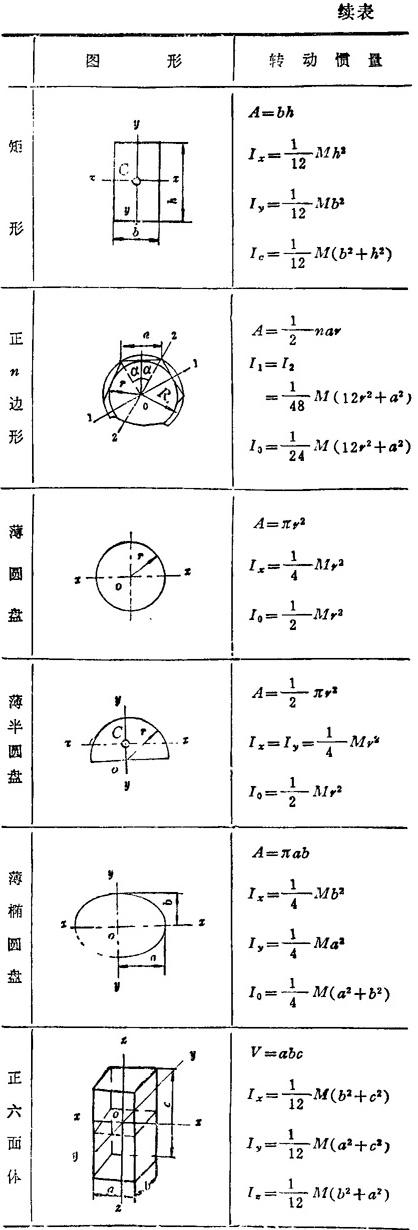
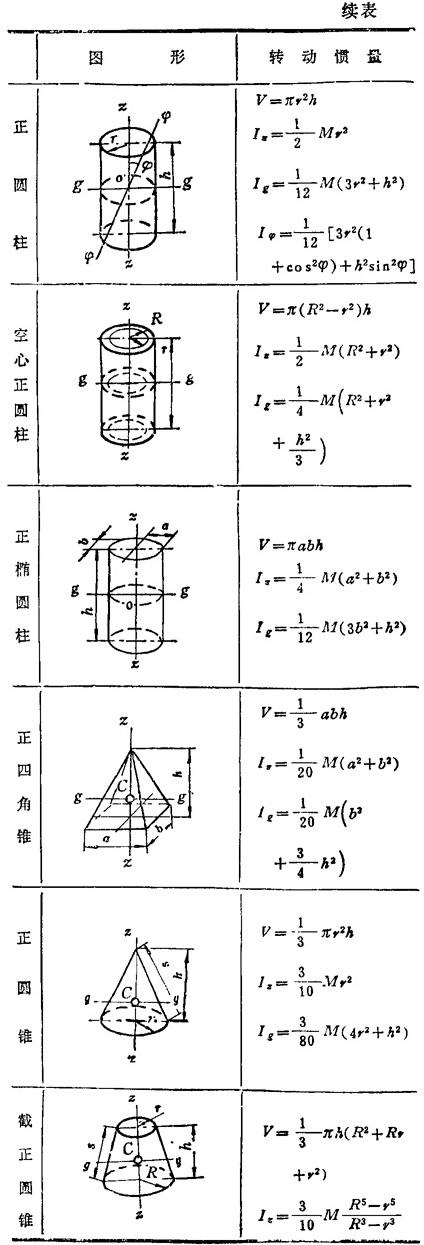
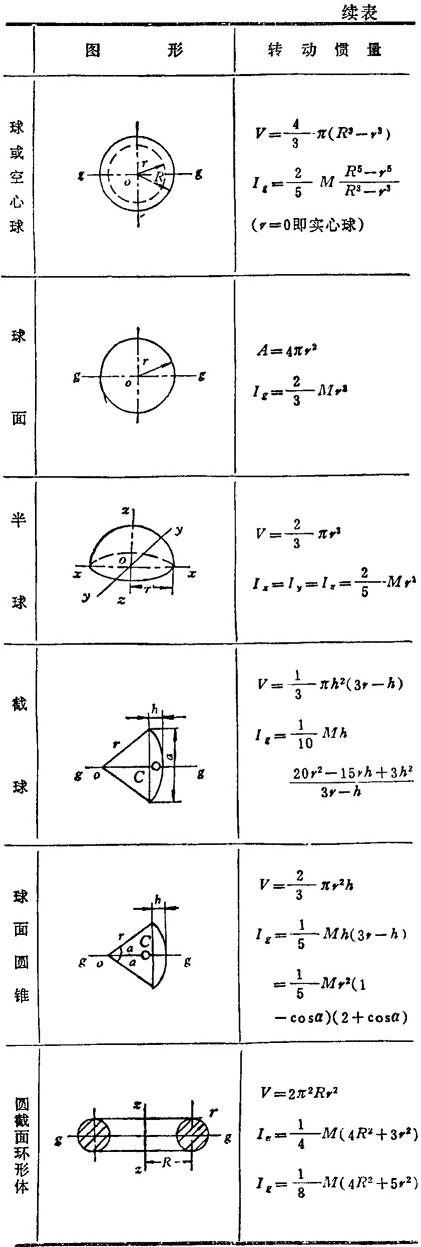
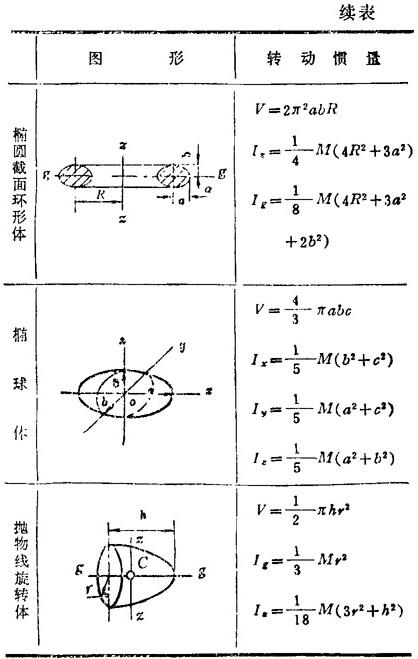
说明：1．A，V——物体的面积、体积；2．M——物体的质量；3．C－－物体的质心；4．平面图形中对点的转动惯量(如I₀，I_c等)，即为对过该点并垂直于图面的轴之转动惯量；5．转动惯量表达式中的质量代换以相应的面积(A)、体积(V)，则为该几何图形的转动惯量。

3．1．3 惯性主轴和惯性主轴坐标系

若I_xy=I_xz=0，则x轴称为刚体过坐标原点Ο的一根惯性主轴；若Οxyz的三根轴都是过Ο点的惯性主轴，则该坐标系称为刚体过Ο点的惯性主轴坐标系；若过质心C的轴为惯性主轴，则该轴称为中心惯性主轴。如果刚体的质量分布具有对称性，则有以下定理存在：

①如果刚体具有质量对称面，则垂直于该对称面的任一轴都是刚体过该轴与对称面交点的一根惯性主轴；

②如果刚体具有质量对称轴，则该轴是刚体过轴上任一点的惯性主轴，而且是过质心的中心惯性主轴。