弹性薄壳

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第154页（5087字）

常见的薄壳结构几何形状，有圆柱壳、圆锥壳、球壳、旋转壳等。薄壳受载变形后，如果中曲面上各点的法向位移均比薄壳厚度小得多，则称为薄壳的小挠度问题。

小挠度薄壳理论简化计算的基本假定：

①平行于中曲面各面的法向正应力，比其它应力小得多，忽略不计。

②变形前与中曲面垂直的线段，变形后仍为与中曲面垂直的直线，且长度不变。

薄壳受外力作用，在微元上的内力有两类：

①使薄壳伸长或缩短的力，称为薄膜力，如图1．3－30(a)所示的N_a，N_β和N_aβ。

②使薄壳弯曲或挠曲的力，包括弯矩，扭矩与剪切力，如图1．3－30(b)所示的M_a，M_β，M_aβ、Qa和Qβ。

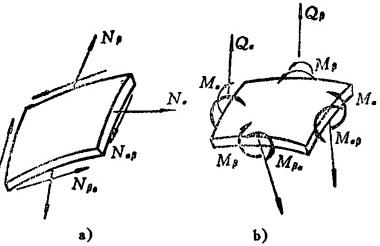
图1．3－30 薄壳的内力

如果薄壳受均匀外力作用，壳的厚度和曲率没有突然变化，并且没有产生弯矩的边界条件(如与其它构件刚性联结)，此时可以忽略弯矩、扭矩和剪力的影响。只有薄膜力作用的薄壳可以仅由静力学方法计算内力，这种简化计算的理论称为薄膜理论或无矩理论。

2．4．1 旋转薄壳的薄膜理论

若壳体中曲面是由一条曲线或直线绕某轴旋转而成的，则称为旋转壳。过旋转轴的平面与中曲面的交线称为子午线。垂直旋转轴的平面与中曲面的交线是一个圆，称为平行圆。

旋转壳受轴对称载荷作用时，其微元内力，如图1．3－31所示，有：沿子午线方向的单位长度拉力或压力N_Φ；沿平行圆方向的单位长度拉力或压力N_θ；沿子午线切线方向的单位面积载荷分量p_1；沿中曲面法线方向的单位面积载荷分量p_n。

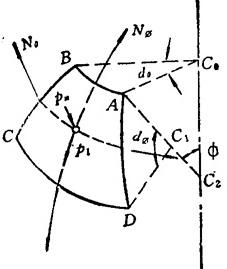
图1．3－31 旋转壳微元的内力

旋转壳薄膜理论的平衡方程为：

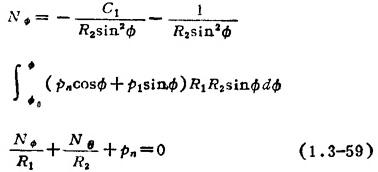
式中 R₁和R₂分别是子午线截面的主曲率半径和与子午线垂直的截面的主曲率半径；C₁是边界Φ₀上单位长度的均布垂直力，见图1．3－32。

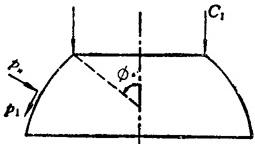
图1．3－32 旋转壳的边界力

由上述二个平衡方程可以求解二个未知内力N_a和N_s。

表1．3－31列出各种旋转壳受轴对称载荷作用时薄膜力和变形的计算公式。

表1．3－31 轴对称旋转壳薄膜力和变形计算公式

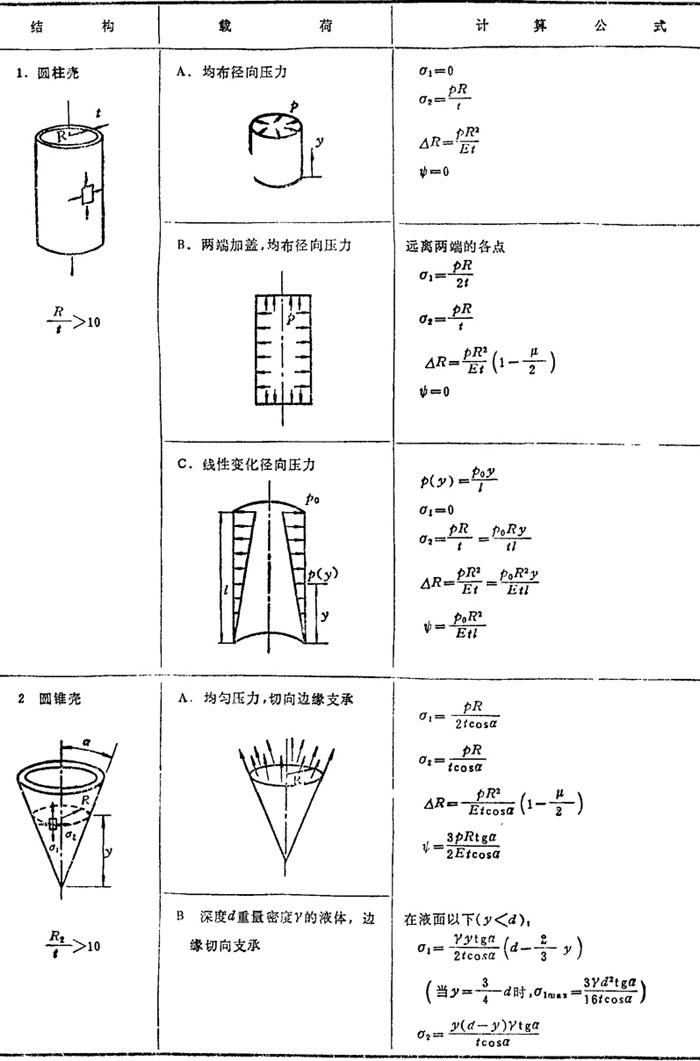
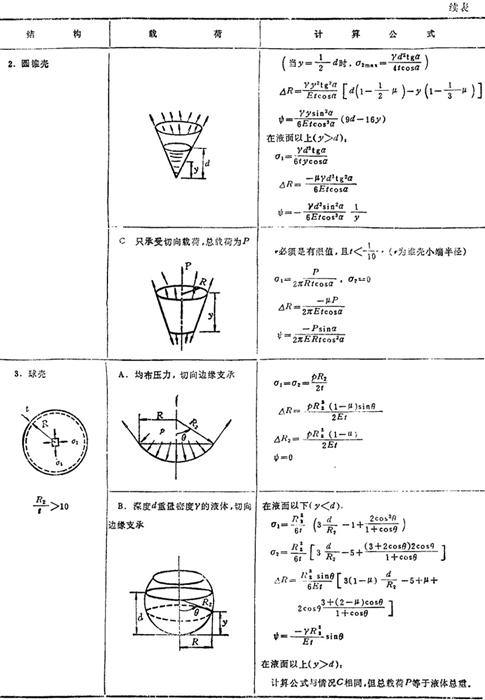
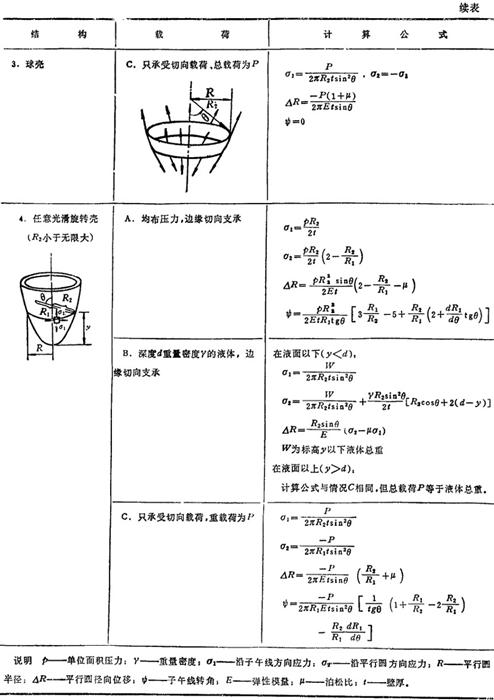
2．4．2 圆柱薄壳的弯曲计算

从结构设计优化来讲，希望弹性薄壳内不产生弯曲作用，而处于均匀面内应力状态，有助于减轻壳体重量。但是，它要求壳体形状、边缘支承和载荷形式满足一定条件。在许多实际壳体结构中，在壳体边缘附近、厚度或曲率半径有突然变化的局部区域，发生弯曲变形。即使是较小的弯矩，也会产生相当大的应力。

受轴对称载荷作用的圆柱壳，微元内力如图1．3－33所示，其平衡方程为：

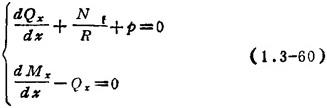
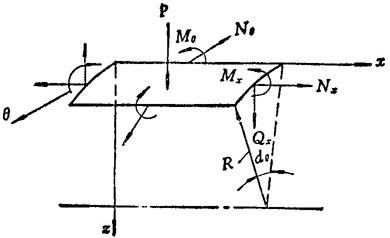
图1．3－33 圆柱壳微元上的内力

当N_x=0，即沿x方向没有拉力或压力时，位移与应变的关系是：

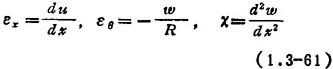
式中 R是中曲面半径；ε_x和ε_s分别是中曲面上沿x方向和θ方向的线应变；x是中曲面沿x方向曲率的变化；ω是径向位移。

内力与位移的关系：

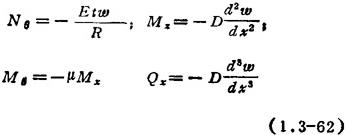
应力与内力的关系：

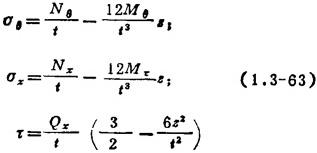
基本方程是：

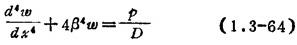
式中：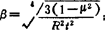

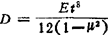
其解为 ω=e^βx(c₁cosβx+c₂sinβx)+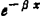(c_。cosβx+c₄sinβx)+f(x) (1．3－65)

式中 f(x)是基本方程的特解；c₁、c₂、c₃和c₄是积分常数，由边界条件确定。

圆柱薄壳的边界条件有：1．自由边：Q_x=M_x=0(如果自由边有单位边长载荷Q和M，则Qx=Q和M_x=M)；2．固定边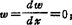： 3．铰支边：ω=M_x=0。

(1)长圆柱壳

如果圆柱壳比较长，则边界影响将很快衰减，基本方程解可近似取为：

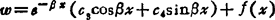
(1．3－66)

研究表明，当βx≥3时，可以作为长圆柱壳计算。若μ=o．3，则长圆柱壳的长度条件为：

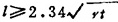
表1．3－32列出不同边界条件下长圆柱壳的Mx、M_θ、Q、θ和N_θ的算式。表中的函数值分别为：

A_βx=e^－βx(cosβx+sinβx)；B_βx=e^－βx(cosβx 5inβx)；Cβx=e^－βxcosβx；D_βx=e^－βxsinβ_x。其值见表1．3－33。

表1．3－32 长圆柱壳的内力和变形计算公式

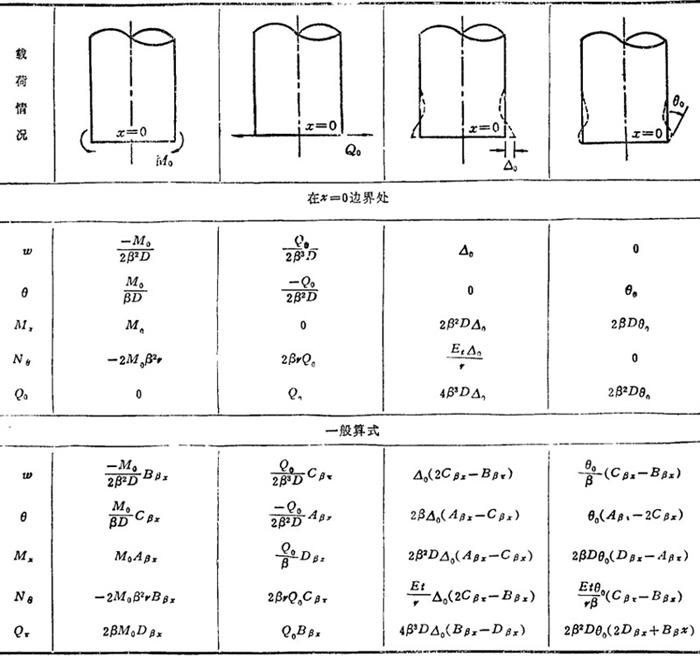
注，表中A_βx、B_βx、C_βt、D_βr之值见表1。3－33。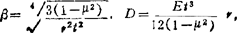－中曲面半径，t－壁厚，μ－泊松比，E－弹性模量。

表1．3－33 A_xβ、B_βx、C_βx、D_βx函数值

(2)短圆柱壳

圆柱壳长度]，应按短圆柱薄壳公式计算。挠度公式可写成：

ω=A₁sinβxsinhβx+A₂sinβxcosh_βx+A₃cosβxsinh_βx+A₄cosβxcosh_βx+f(x) (1．3－67)

不同边界条件的解见表1．3－34。

表1．3－34 短圆柱薄壳的计算公式

2．4．3 旋转薄壳的弯曲计算

旋转薄壳受轴对称载荷作用时微元内力如图1．3－34所示。

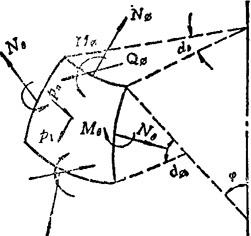
图1．3－34 旋转薄壳受轴对称载荷时的内力旋转薄壳微元的平衡方程：

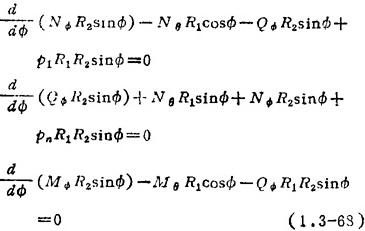
式中 p_n、p₁分别是法向和切向压力。

在Φ角平行圆以上壳体部分沿轴向的平衡方程

式中 c1为边界Φ₀上单位长度分布载荷沿轴向方向的分量。

位移与应变、角位移与曲率间的关系：

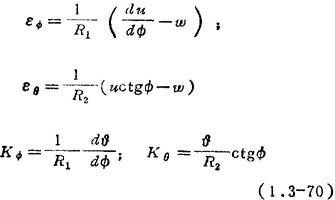
式中 切线角位移 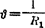(v－)．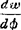

内力与变形的关系：

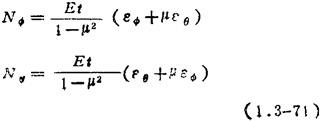
M_Φ=－D(K_Φ+μK_θ)

M_θ=－D(K_θ+μK_Φ)

边界条件：

固定边：θ=0_，ε₂=0(u=0) (1．3－72a)

自由边：M_Φ=0，N_Φ=0(或Q_Φ=o) (1．3－72b)

封顶壳：在Φ=0处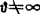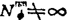， (1．3－72c)

轴对称边界载荷作用下冠状球壳的内力和边缘处径向位移δ与转角φ的计算公式见表1．3－35；轴对称边界载荷作用下圆锥壳的内力和边缘处径向位移δ与转角ψ计算公式见表1．3－36。

表1．3－35 冠状球壳内力和边缘变形计算公式

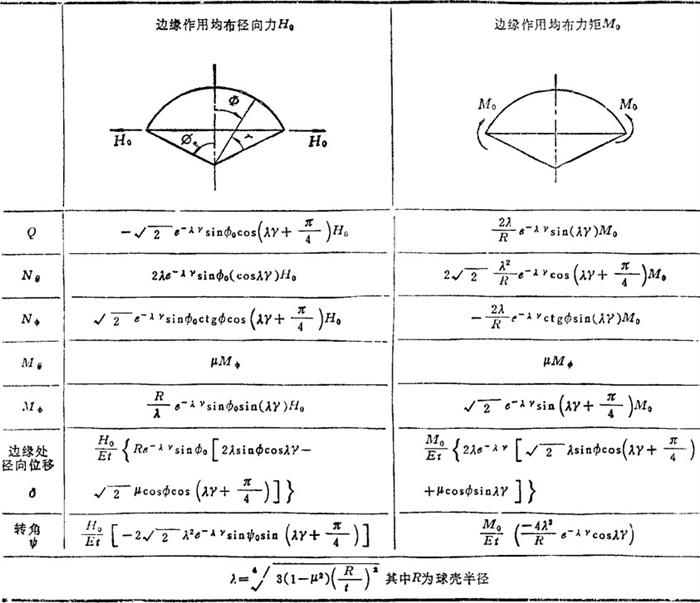
表1．3－36 圆锥壳内力和边缘变形计算公式

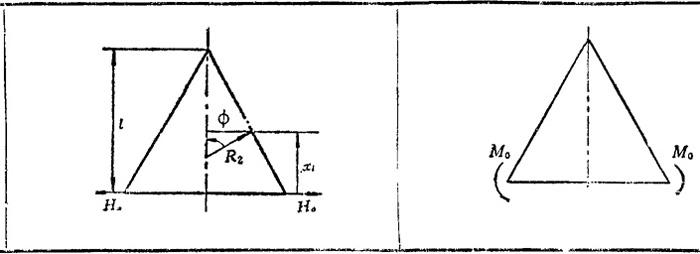
弯曲计算表明，边界约束反力对壳体内力和变形的影响，随边界的距离增加而迅速衰减。工程计算中，为避免有矩理论精确求解的困难，通常采用如下算法：

①按无矩理论求解，作为壳体在边界邻近区域以外各处的近似解。

②将上述无矩理论的解，叠加上仅有边界约束反力作用的有矩理论解，作为壳体在边界邻近区域的近似解。

③根据边界的位移约束条件，即

δ_o+δ_M+δ_P=△

ψ_o+ψ_M+ψ_P=ψ

计算壳体的边界约束反力。

式中 △为壳体边界处允许的平行圆径向位移；ψ为壳体边界处允许的子午线转角；δ和ψ的下标Q、M、P分别表示在边界处壳体因约束反力Q、M和载荷P引起的径向位移和转角。

这里以图1．3－35所示半球壳封头的长圆柱壳容器应力分析为例，说明组合壳的求解方法。

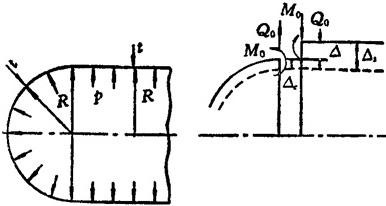
图1．3－35 半球壳封头的圆柱壳容器

半球壳和圆柱壳半径为R；厚度相同，为t；材料相同(弹性模量E和泊松比μ)；承受内压力p。

先将半球壳与圆柱壳分开，按无矩理论计算。

由表1．3－31查得：

半球壳

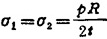
与圆柱壳连结的球壳端部，半径增大

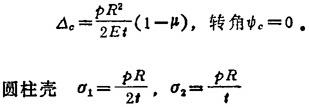
与半球壳连结的圆柱壳端部，半径增大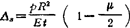，转角φ_s=0。

由此可见，由薄膜应力产生的这两部分半径增大的差值为：

实际上，半球壳与圆柱壳是连续的，它是通过接合处单位周长的剪力Q₀和弯矩M_o的相互作用而保持在一起的。这些相互作用力和力矩将使半球壳和圆柱壳在接合处附近引起局部弯曲应力。由表1．3－35和表1．3－32可以算出，当半球壳(Φ_o=90°)和长圆柱壳的半径R和厚度t相同时，在接合处两种壳由剪力Q₀产生的径向位移和转角相同。因此，当M_o=0而Q_o值能使圆柱壳边缘产生挠度为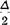时，就能满足两种壳在接合处的变形连续条件。由表1．3－32得到

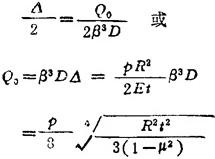
当Q₀值求出后，即可由表1．3－32求得圆住壳离接合处距x的任意点纵向应力：