热传导过程

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第215页（3376字）

2．2．1 傅立叶导热定律

傅立叶总结了均质固体中的导热规律。即：发生纯导热现象时，单位时间内导过垂直于热流方向的面积dA的热流量其数值与而积dA及该处温度梯度的绝对值成正比，方向与温度梯度相反。傅立叶导热定律表达式有：

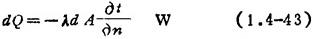
式中 dQ为单位时间内通过面积dA的导热量，或称导热热流量，W；dA是与热流方向垂直的微元导热面积，m²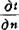；是在等温面dA处的温度梯度，℃／m；λ为比例系数，称导热物体的导热系数，W／(m·℃)。

如整个导热面积A是等温面，且面上各点的温度梯度均匀，则可写成：

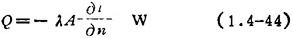
至于热传导的热流密度(简称热流)，可表示为：

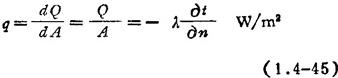
傅立叶导热定律是解决所有导热问题的基础，它不但适用于固体中的导热，而且适用于液体和气体中的导热：不但适用于一维温度场，而且适用于多维温度场，不但适用于稳定温度场，而且适用于不稳定温度场。

2．2．2 导热系数λ

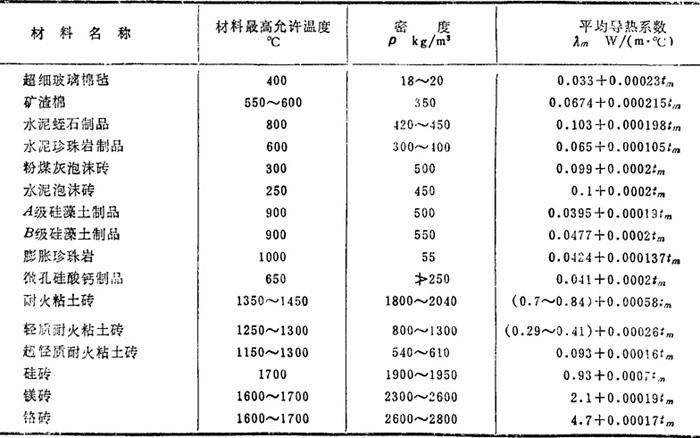
傅立叶导热定律表达式中的“λ”是物体的物性参数之一，不同的物体具有不同的λ值。一般说来，λ_固体＞λ_液体＞λ_气体。空气及其它气体的导热系数见表1．4－10；一些常用液体的导热系数见表1．4－11：某些金属及非金属材料的导热系数见表1．4－12；各种保温耐火材料的算术平均导热系数λ_m与算术平均温度t_m之间的关系见表1．4－13。

表1．4－10 气体的物性参数

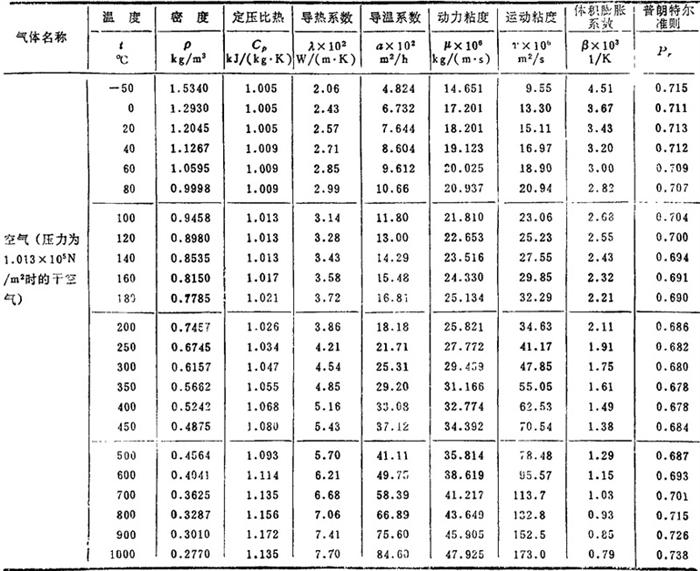
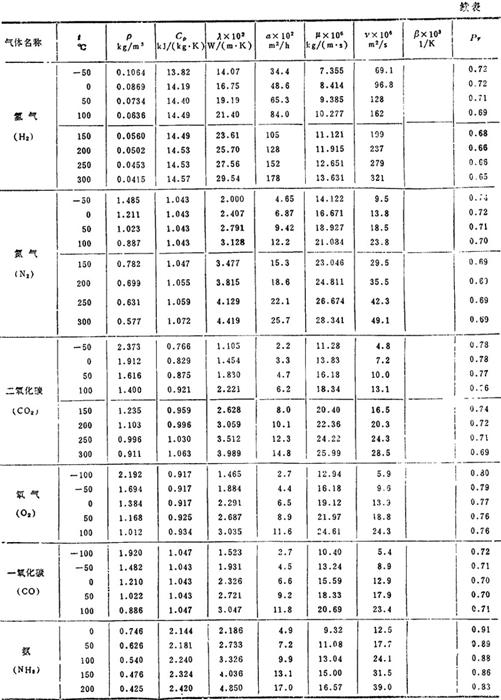
表1．4－11 液体的物性参数

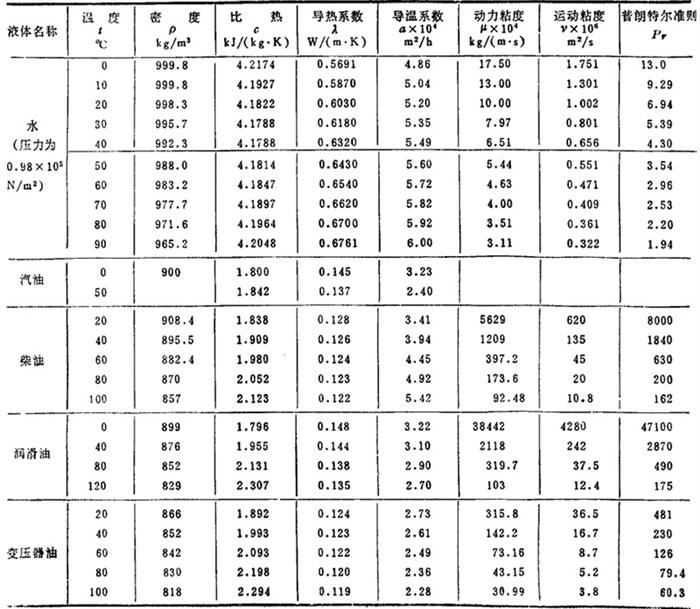
表1．4－12 金属及非金属材料的物性参数

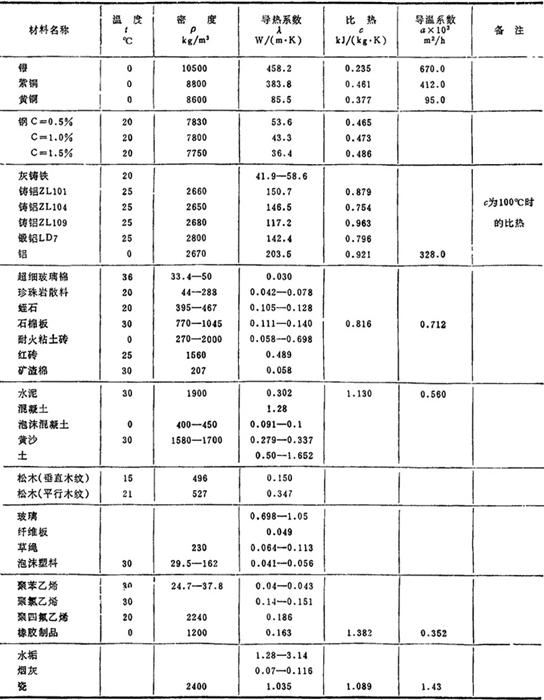
表1．4－13 几种保温、耐火材料的导热系数与温度的关系

2．2．3 多维导热过程的数学描写

求解导热问题的主要目的，往往是求物体内的温度场，其次是求导热量。对于多维的，特别是不稳定的及物体中有内热源的导热问题，必须先建立数学模型(即导热微分方程式)，然后结合单值性条件才能求解。

根据傅立叶导热定律及能量守恒定律，在某些简化假设条件下，可推得

直角坐标中的导热微分方程式：

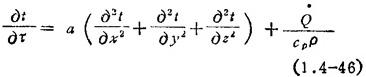
式中 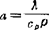，是导热物体的综合性物性参数，称作导温系数或热扩散率，m²／s；Q是导热物体的内热源，即发热量，W／m³。

圆柱坐标中的导热微分方程式：

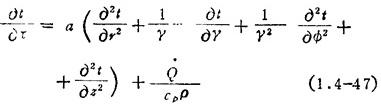
式中 r为径向坐标；z为轴向坐标；Φ为圆周方向坐标。

球坐标中的导热微分方程式：

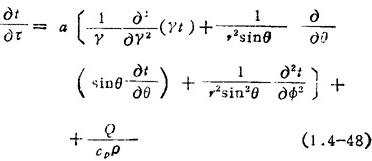
2．2．4 一维稳定导热解

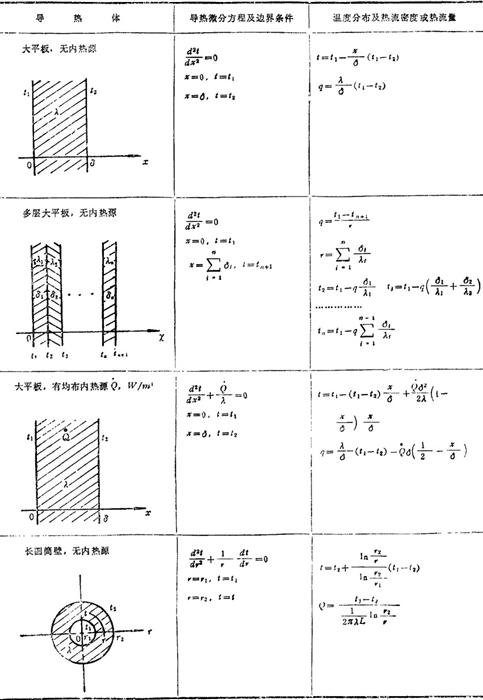
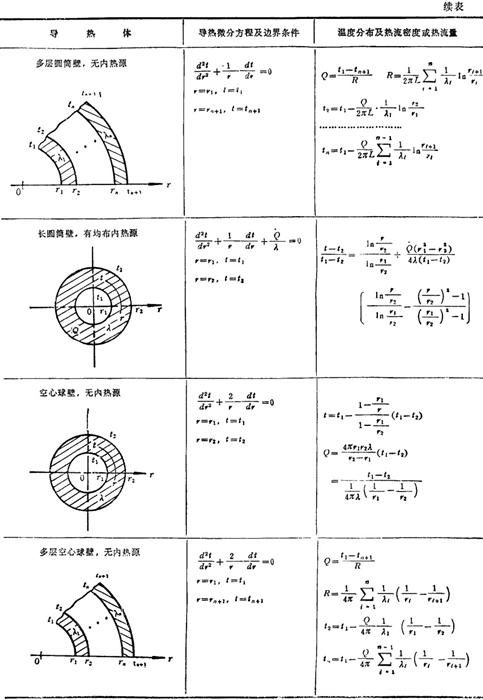
大平板、长圆筒壁及空心球壁中的导热，是典型的一维导热。因为温度t只沿厚度方向x或半径方向r变化。在稳定温度场及常物性条件下，无内热源及有均布内热源两种情况的解法分别列于表1．4－14。

表1．4－14 一维稳定导热解

2．2．5 二维稳定导热的近似解法

导热微分方程式的积分求解(即分析解法)，通常只对形状简单、边界条件不复杂的情况才有可能。对于几何形状和边界条件较复杂的多维温度场，一般只能应用近似解法或模拟法求解。这里主要介绍近似解法中的形状系数法和数值解法中的有限差分法，并限于二维无内热源的稳定温度场。

形状系数法：在这类问题中，常遇到的是有两个等温表面的二维导热系统，而且主要关心的是在这两个等温表面之间所传导的热流量Q。其形式一般可以整理成

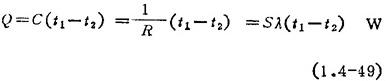
式中 t₁、t₂为两等温表面的温度，℃；C为导热系统的热导，W／℃；R为导热系统的热阻。℃／W；S为导热系统的形状系数，m。

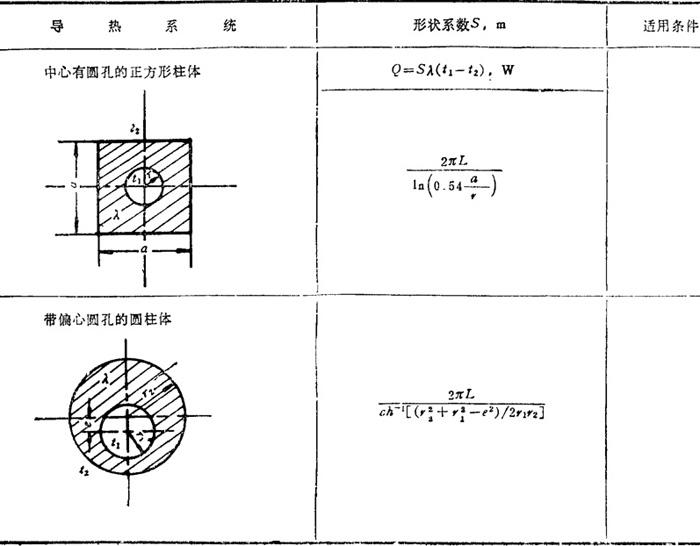
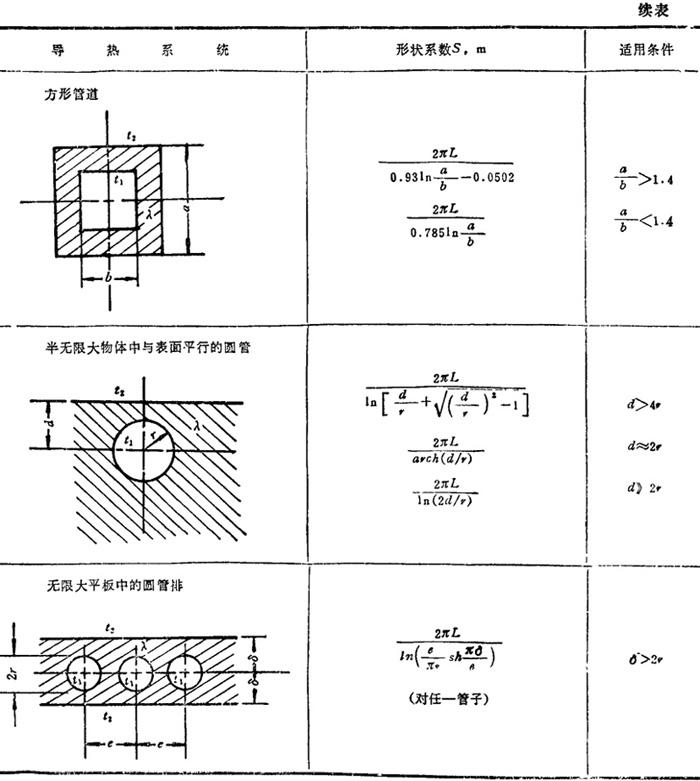
表1．4－15给出一些有两个等温表面的二维导热系统的形状系数的计算式，这些公式是在导热系数作为定值的条件下导得的。实际上，材料的导热系数随温度而变，计算时可取用两侧温度范围内的算术平均导热系数值。表中的L为垂直于图面方向上物体的长度(》图面上各尺寸)，m。

表1．4－15 几种二维导热系统的形状系数S

有限差分法：根据有限差分法的基本原理，把欲分析求解的二维温度场，用长宽相同的小方格划分成为很多单元，如图1．4－4所示(每单元的中心称为节点)。在温度场稳定条件下，利用傅立叶导热定律及能量守恒定律可以证明：任一节点的温度必等于四邻各节点温度的平均值，即

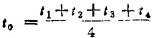
也就可得

t₁+t₂+t₃+t₄－4t₀=0 (1．4－50)

这是对某一节点的温度平衡方程式。若有N个节点，则可写出N个方程，联立求解N个方程即可求得每一节点的温度值，同时也了解了温度分布情况。所以，应用有限差分法能使难以求解的导热微分方程式变为便于求解的一组代数方程式。

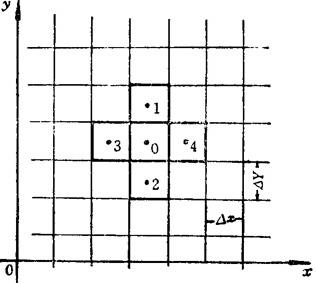
图1．4－4 二维温度场中的有限单元

求解联立方程组，一般有松弛法、高斯—赛德尔迭代法和逆矩阵法等(见本篇第一章6．2)，使用松弛法的步骤如下2

①根据已知条件(如边界条件已知)，初估各节点温度，如t₁、t₂、……t_n。

②把初估值代入公式(1．4－50)(注意，此公式中“0”代表某节点，而“1”、“2”、“3”、“4”代表其上、下、左、右各节点)，对各节点进行计算。因所估值不司能精确，故等号右边并非零值而为余数Q′，即t₁+t₂+t₃+t₄－4t₀=Q′。求出各节点的余数Q′₁、Q′₂、……Q^′_n。

③对各有余数的节点，以其余数Q′值的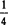一维和三维温度场则为1／2和1／6)，作为对应节点初估温度的修正值。修正值所取的正负号与余数一致。如余数为Q′=－20，则初估温度应加－20／4=－5。

④以修正后的各节点温度，再次计算各节点的余数，并重复进行，直至全部余数接近于零。

求得各节点可代表温度分布情况的最后的温度值，即可进一步计算导热量。每单位物体高的导热量为

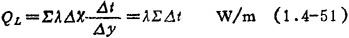
式中的△t，可取物体任一侧(高温一侧或低温一侧)各单元体的温差。