稳定裕量

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第398页（1219字）

图1．9－33所示是开环幅相频率特性曲线对(－1，j0)点的位置与对应的系统单位阶跃响应示意图。图中各系统的开环传递函数在右半S平面的极点数P皆为零。由图可见，当开环幅相曲线包围(－1，j0)点时，对应的系统单位阶跃响应h(t)发散，系统不稳定；当开环幅相曲线通过(－1，j0)点时，对应的系统单位阶跃响应h(t)呈等幅振荡；当开环幅相曲线不包围(－1，j0)点时，系统稳定。但由图(c)、(d)可知，开环幅相曲线距(－1，j0)点的远近程度不同，系统的稳定程度也不同。开环幅相曲线距(－1，j0)点越远，闭环系统稳定的程度愈高。通常以稳定裕量来表示系统的稳定程度。系统的稳定裕量(也称稳定裕度或稳定余量)包括幅值裕量和相角裕量。

图1．9－33 系统的相对稳定性

幅值裕量(增益裕量)的定义：

相位为－180°的频率(ω_g)的幅值|G(jω_g)H(jω_g)|的倒数，用kg表示，即

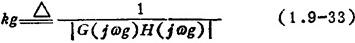
kg的，物理意义是如果系统的开环增益再增大kg倍，则系统处于临界稳定状态。

相角裕量的定义：

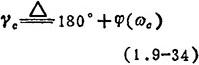
上式的φ(ω_c)是开环频率特性的幅值|G(jω_c)H(jω_c)|=1时的相角，一般为负值。相角裕量的物理意义是，如果φ(ω_c)再滞后γ_c时，系统就处可临界稳定状态。

图1．9－34所示为在开环幅相图上表示的系统的幅值裕量和相角裕量。在该图与式(1．9－33)和(1．9－34)中，ω_c和ω_g分别称为幅值穿越频率和相角穿越频率。

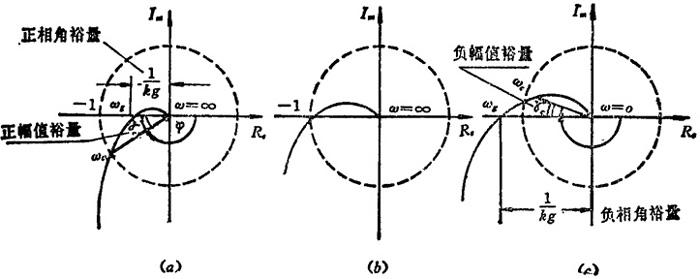
图1．9－34 在开环幅相图上表示的稳定裕量

幅值裕量和相角裕量也可以在对数坐标图上表示，如图1．9－35所示。在对数坐标图中，幅值裕量kg的分贝值为

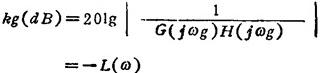
相角裕量为 γ_c=180°+φ(ω_c)

图1．9－35 在开环对数坐标图上表示的稳定裕量

对于最小相位系统⁽¹⁾，当幅值裕量kg(dB)，相角裕量γe均为正值时，系统是稳定的。图1．9－34和1．9－35中图(a)所示的系统是稳定的，图(b)、(c)所示的系统是不稳定的。系统的稳定裕量过大会使系统响应变慢。经验证明，当取kg=(10～20)dB，γo=40°～60°时，系统的综合性能较好。