相似理论及其在模化设计中的应用
出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第716页（4558字）
5．1．1 相似理论
相似方法是把个别现象的研究结果推广到所有相似现象的科学方法，相似理论是现象模拟和研究自然界及工程中相似现象的基础。利用相似理论，使运用简单的模型实验去研究复杂工程问题成为可能。在机械设计中，相似理论还可用于产品系列设计和成本估算等方面。
(1)相似
一组物理现象，其基本参数之间有固定成比例的数量关系，称为相似。相似又分同类相似和异类相似。
同类相似，即各物理现象可以用完全相同的数学方程来描述，其中所含的物理量都具有相同的性质(同名量)，同名量之间在对应的空间点和时间上满足相似的比例数量关系。例如机械零件或部件的模型实验，一般属于同类相似。
异类相似，即各物理现象之间在形式上可以用完全相同的数学方程来描述，但其中所含的参量具有不同的性质。例如流体的压力场及导体的电场，当能用相同形式的数学方程表达时，则为异类相似或类似。
这里主要介绍同类相似的基本理论。其基本原则，也可用于异类相似中。
(2)相似比
在两个相似系统中，各个同一性质的同名参量，在两个系统相应的位置和时间上(对于非定常过程)的比值，称为相似比。对于不同的参量，相似比一般是不同的。
互相独立的基本物理量长度L、力F、时间t、温度T、电量q等形成的相似比，称为基本相似比，其中长度、力、时间为基本量纲。
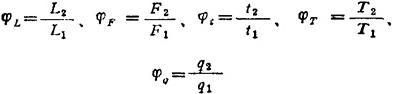
根据量纲理论由基本物理量导出的相似比，称为导出相似比，如速度、加速度的相似比。在机械系统中，常用的相似有：几何相似，即系统中各对应长度成比例，各对应角相等；力相似，即几何相似的系统各对应点的力方向一致，大小成比例；运动相似，即几何相似的系统各对应点上速度、加速度方向一致，大小成比例。
(3)相似准则和相似指标
各物理现象根据其物理关系式可推导出由物理量组成的无量纲数群，它在该现象的不同点上具有不同的数值，当两现象相似时，在对应点上有相同的数值，此无量纲数群即称为相似准则。
与相似准则各参数对应的相似比组成的关系式，称为相似指标。
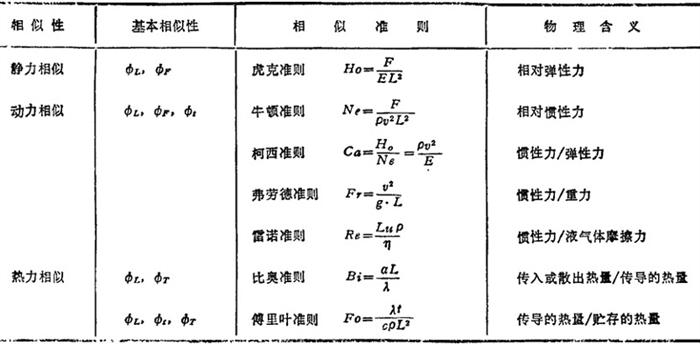
例如，分析质点运动系统时，由物理关系式V=L／t，其相似准则是无量纲数群Vt／L，而相似指标是φVφt／φL。工程中常用的相似准则见表3．1－10。
表3．1－10 工程常用相似准则
(4)相似三定理
相似第一定理(相似正定理)：彼此相似的现象必须具有数值相同的同名相似准则，且相应的相似指标为1。
相似第二定理(Π定理)：一个物理系统有n个物理量，其中k个物理量的量纲是相互独立的，则物理量可表示为(n－k)个相似准则Π1、Π2…Πn－k的函数关系：
f(Π1、Π2……Πn－k)=0
相似第三定理(相似逆定理)：对同一物理现象，如果单值条件(几何条件、介质条件、初始条件、边界条件)相似，由单值条件的物理量所组成的相似准则在数量上相等，则现象相似。
5．1．2 模型实验的模化设计
(1)实验设计规则
模型实验的模化设计应遵循的规则包括：1．模型与原型实物必须是几何相似的；2．描述模型现象的数学方程式应当与原型实物现象的相同；3．在模型与实物中进程的初始条件及边界条件相似；4．参与这两种现象中的诸同名参量应是相似的。但是，在实际工作中要保持完全的相似条件有时是很困难的，因而往往采取保留其主要的相似条件而忽略一些次要相似条件的方法，即近似模型研究法。
对于测定与应力、变形有关性能参数的模型实验，一般要求模型材料的弹性模量较小，在一定载荷下变形大，测量精度高，并且易于加工和成型，具有一定的强度，以及良好的化学稳定性和耐腐蚀性，如采用硬质聚氯乙烯、有机玻璃、铝粉增强环氧树脂等。为便于测量，应力和变形值不可过小，但应控制在弹性范围内，应力不应超过许用值。
模型的工作条件，常用各种方法模拟，有时需进行适当简化。例如，加力可采取叠加或代用方法(如用液压、气压力代替原型中的机械力等)。
(2)相似比方程
模化设计的关键是根据相似理论求出各参数的相似比。为此，需先建立相似比方程，然后求解得出相似比。相似比方程可以利用下列几种方法建立；
①相似准则法。在工程设计中，为了使供设计使用的性能数据具有通用性，往往采用无量纲的分析方法，从而得到一系列的无量纲的数群。这个无量纲的数群，就是相似准则。根据第一相似定理，就可得到相似比方程。例如在流体动压润滑径向轴承中，采用了无量纲压力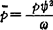
(其中p为油膜压力，φ为轴承相对间隙，η为润滑油动力粘度，ω为轴颈角速度)，根据第一相似定理，可得相似比方程：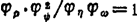
②方程分析法。即由参数关系式求相似比方程。如果系统的物理或几何参数关系可以用下列方方程表达：
A=CXmYnZp
则可证明，相似比方程为
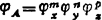
式中 A为因变量参数；C为常数；X、Y、Z为自变量参数；m、n、p为指数，可见，当两系统相似时，相似比方程中各参数的相似比对应于原参数关系式中的参数，而常数不再出现。
③量纲分析法。根据物理关系式方程等号两边量纲相同的原理，可利用物理量的基本度量单位长度L，时间t及力F(或质量M)，推算出指数未定的物理方程，从而建立相应的相似比方程。
例如，知道机床的强迫振动频率f与长度L(m)，材料密度p(kg／m3)及弹性模量(N／m2→(kg·m／s2)／m2)有关。即
f=F(L，ρ，E)
于是得关系式f=cLαρβEγ(其中c为常数，α，β，γ为指数)。相应量纲方程为：
t－1=Lα(M／L3)β(MLt－2／L2)γ
根据两边量纲相同的原理，可得下列线性代数方程组；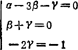
并解得：α=－1，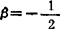
，
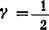。故机床床身的强迫振动频率方程为：
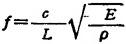
由此得出两系统相似时的相似比方程：
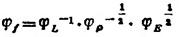
量纲分析法适用于上述物理关系式为简单指数形式的情况，要求初步分析正确全面，否则得不出正确的结果。
(3)模型实验的模化设计举例
例3．1－2 现欲建立一台流体动压润滑滑动轴承模拟实验装置。其实验模型尺寸为原型的1／4。实验测量内容为：压力分布p、承载能力F、摩擦系数f和润滑油流量q。求各参数的相似比。
解：根据流体动力润滑分析，可得如下无量纲数群：
无量纲压力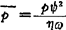 
无量纲承载能力系数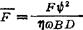 
无量纲摩擦系数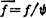 
无量纲润滑油流量系数q=q／φωD3。
式中 B、D分别为轴承的宽度和直径，因而可得相似比方程组：
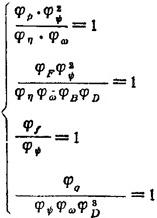
根据几何相似条件，上式中φD=φB=4。则表达实验结果的相似比φp、φF、φl及φα可根据φω、φφ及φη求得。例如当实验模型采用与原型相同的角速度(φω=1)、相对间隙(φφ=1)及润滑油(φη=1)时，可得：φp=1、φF=16、φl=1、φυ=64。
上述模型设计虽然满足了要求的主要相似条件，但不可能做到绝对准确。例如，由于实验模型与原型散热条件不同，即使采用同一牌号的润滑油，由于温度的差异，使得粘度不可能完全相同(φη≠1)，因而带有一定的误差。
例3．1－3 如图3．1－11所示压力机，实验模型的尺寸为原型机器实物的一半，相应零件材料相同，根据立柱拉伸强度和横梁弯曲强度条件求模型实验应加的载荷Q。
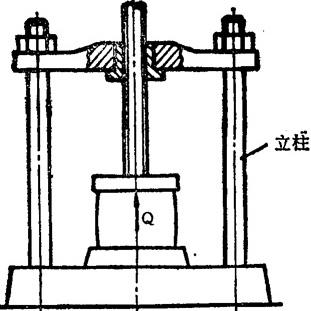
图3．1－11 压力机简图
解：采用方程分析法建立相似比方程，求解载荷相似比φp。
立柱拉伸强度关系式：
式中 d为立柱直径。可得相似比方程：
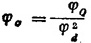
由题意已知φd=2(几何近似)．φσ=1(材料相同)，故可算出φo=4。
横梁弯曲强度关系式：
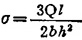
式中 l、b、h分别为横梁的跨度、宽度与高度。可得相似比方程
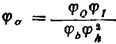
由于已知φσ=1，φl=φb=φh=2，故可得φo=4。
由此可知，该实验模型不论是对立柱或者横梁进行强度分析，其实验载荷均采用原载荷的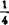
。
5．1．3 异类相似模型
表3．1－11列出两种异类相似模型的举例。采用这种模型，可以通过实验或计算分析的方法求得原型的性能规律。
表3．1－11 异类相似模型举例
