最优化设计的基本概念

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第722页（4519字）

最优化设计方法，就是将工程设计问题转化为最优化问题，然后选择适当的最优化方法，利用电子计算机从满足要求的可行方案中自动寻找最优的设计方案。

所谓最优化问题，就是如何从一切满足要求的可行方案中寻找达到预期目标的最优方案问题。用数学语言表达，就是求某些变量的函数值在一定条件下的极值(极小值或极大值)的问题．例如，有一变量为X(x₁，x₂)的函数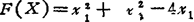：+4，求在满足g₁(X)=x₁－x₂+2≥0、g₂(X)=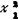－+x₂－1≥0、g₃(X)=x₁≥0、g4(X)=x₂≥0的条件下，函数F(X)值为最小时的变量X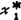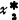^*(，)值。这样的问题，就是最优化问题。这里，所要求出的变量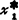、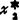相当于所要选择的方案的参数，在工程设计中称为设计变量；所要求出的函数的极值F(X^*)相当于预定的最优化目标；所需优化的变量的函数F(X)称为目标函数；所要满足的条件g_l(X)≥0(j=1、2、3、4)称为约束条件；而且通常将问题写成如下形式，即

求变量 X(x₁，x₂)

极小化目标函数 F(X)=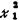+－4x₁+4

满足约束条件 g₁(X)=x₁－x₂+2≥0

g₂(X)=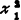－+x₂－1≥0

g₃(X)=x₁≥0

g₄(X)=x₂≥0

这种表达式称为最优化问题的数学模型，求出的解X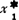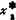^*(， )称为最优解。图3．2－1为它的空间图形：目标函数F(X)是一抛物面；约束条件g₁(X)是一直立的约束平面；约束条件g₂(X)是直立的约束抛物面；约束条件g₃(X)和g₄(X)为坐标x₁、x₂≥0区域的空间。图中F(X)曲面上的虚线表示用若干个平行于x₁ox₂平面来切割曲面时所得的曲线，即相应于F(X)=0，1／4，1，2¹／₄，4…等常数时的F(X)曲线。这些曲线称为等值线。图中x₁ox₂平面上的同心虚线圆族，即为F(X)上的一系列等值线的投影。它表示目标函数值的变化情况，由外向内，目标函数值逐渐变小。图中还显示出在约束范围内，F(X)在切点X^*处具有最小值，也就是极小化目标函数F(X)的最优解为X^*(， )。

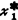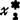图3．2－2为图3。2－1在x₁Ox₂平面上的投影图。图中阴影线范围内的任一点(包括边界点)都满足约束条件，阴影线范围内的区域称为可行域，范围外的区域称为非可行域。在可行域内，目标函数最小值的点就是切点X^*，所以X^*即为最优解。图中X^*的坐标为(0．58，1．34)，目标函数最小值F(X^*)=3．80。从图中还可以看出，如果该问题没有约束条件限制，则最优解为X^{* *}，它的坐标为(2，0)，目标函数值为0。

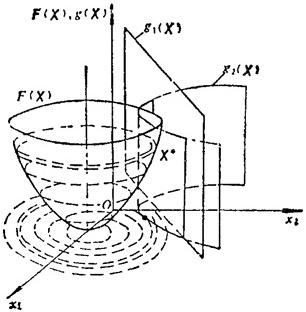
图3．2－1 空间图形

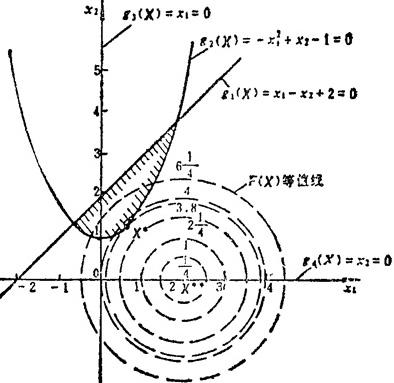
图3．2－2 平面图形

利用上述概念即可将机械设计问题转化为最优化问题求解。例如，设计一两端为固定支承的圆柱形螺旋压缩弹簧，如图3．2－3。弹簧的工作载荷F=680N；载荷作用频率fr=25H_z；最大变形量λ=16．59mm；材料为50CrVA钢丝；材料的密度为ρ=7．8×10^－6kg／mm³。弹簧的结构要求满足：钢丝直径3mm≤d≤9．5mm；弹簧外径30mm≤D≤60mm；工作圈数n≥3；旋绕比C≥6；弹簧两端支撑圈(死圈)的总数n=2。设计要求在满足强度、刚度和其他性能限制的条件与结构条件下，选择弹簧钢丝直径d、弹簧平均直径D₂、工作圈数n，使弹簧的重量最轻。其设计计算步骤为：

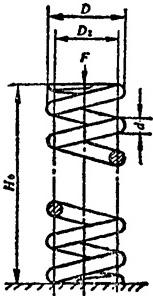
图3．2－3 圆柱形螺旋压缩弹簧的主要尺寸与受力简图

弹簧的重量计算式为

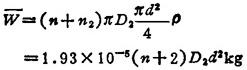
弹簧设计所要满足的条件为：

①强度条件。按机械零件计算公式，弹簧的剪应力

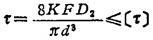
式中K为弹簧曲度系数，其近似公式为

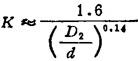
代入上式可得强度条件为

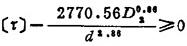
②稳定性条件。由于弹簧两端为固定支承，所以稳定性条件是应使高径比满足H₀／D₂≤5．3。其中H₀=(n+n₂－0．5)d+λ_b，为弹簧自由高度；λ_b为弹簧从自由状态到各弹簧圈完全并紧时的轴向极限变形量(一般取λ_b=1．1λ)，于是，稳定性条件为

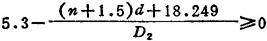
③无共振条件。为了避免弹簧发生共振，应使弹簧的自振频率f远大于工作频率f_rr通常要求f≥15f_r。由于圆柱形压缩螺旋弹簧的自振频率

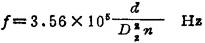
所以无共振条件为 f－15f_r≥0 即

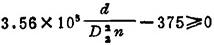
④最大变形条件。为保证弹簧在工作载荷作用下的变形量不超过其许用变形量，必须使工作载荷F不超过对应于许用变形量的最大载荷F_a，即保证F≤F_a。由于

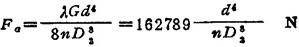
所以最大变形条件为 F_a－F≥0 即

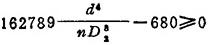
⑤结构条件。根据结构要求，可得结构条件：

n－3≥0；D₂－6d≥0；d－3≥0；

9．5－d≥0；(D₂+d)－30≥0_；60－(D₂+d)≥0

从以上可以看出，设计指标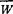和所要满足的各约束条件，都是设计变量d、D₂和n的函数。因此，弹簧最优化设计的数学模型为：

求设计变量 d、D₂和n

极小化目标函数 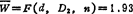×10^－5(n+2)D₂d²

满足约束条件

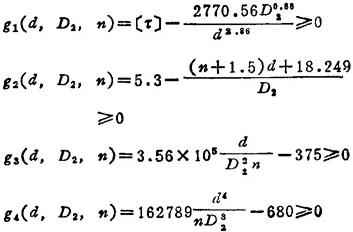
g₅(d，D₂，n)=n－3≥0

g₆(d，D₂、n)=D₂－6d≥0

g₇(d，D₂，n)=d－3≥0

g_a(d，D₂，n)=9．5－d≥0

g₉(d，D₂，n)=(D₂+d)－30≥0

g₁₀(d，D₂，n)=60－(D₂+d)≥0

这种具有三变量、十个不等式约束条件的最优化设计问题，若采用图解分析法求解则十分困难，因为除了要在三变量设计空间作出一系列等值面外，还要作出十个约束面。因此，一般机械优化设计必须采用适当的最优化方法，利用电子计算机来自动寻找最优方案解。但是，对于n个设计变量的最优化设计问题，其数学模型的几何意义仍可从两个变量的举例来类推。一般n个设计变量的优化设计问题的数学模型为：

求设计变量 X(x₁，x₂，…xn)

极小化(或极大化)目标函数 F(X)=F(x₁，x₂，…x_n)

满足约束条件 g_l(X)=g_l(x₁，x₂，…x_n)≥0，j=1．2，…，m

h_l(X)=h_l(x₁，x₂，…x_n)=0，j=(m+1)，(m+2)，…，pa_l≤x_l≤b_l，i=1，2，…n

式中 X是以x₁、x₂，…x_n等n个设计变量为坐标分量的一个设计点；F(X)为含有设计变量的目标函数；gl(Z)≥0，为m个不等式约束条件；hl(X)=0，为p－m个等式约束条件(通常可以只有不等式约束条件，也可以只有等式约束条件，在有些情况下还可没有约束条件)；α_l≤x_l≤bl，为设计变量许可变化范围，b_l、a_l为其上下限(有些问题也可无此限制)。

含有n个设计变量的优化设计问题的数学模型的几何意义、可以从如下方面来理解：

①n个设计变量组成一个n维的设计空间，它们的一组确定值就相当于n维空间中的一个点，即代表一个设计方案。

②每一个不等式约束的极限值表示n维空间中的一个超曲面(即该曲面存在于三维以上高维抽象空间)。这些曲面将设计空间分成“可行域”与“非可行域”两部分。满足不等式约束条件，就是设计点必须在“可行域”中。

③每一个等式约束表示n维空间的一个超曲面。满足一个等式约束，就是设计点必须在那个超曲而上；满足全部等式约束条件，就是设计点必须在那些超曲面共同相交处。

④设计变量的上、下限的约束条件，在n维空问组成一个高维体。满足这个约束条件，就是设计点必须在这个高维体中。

⑤目标函数取一定值时，就在n维空间中形成一个等值超曲面，一系列等值超曲面标志着目标函数的变化规律。

最优化设计的任务，就是要在n维空间寻找一个设计点，使它既能满足约束条件，又位于最小(或最大)等值超曲面上。该设计点，就是所要求的最优方案。

综上所述，最优化设计包括两部分内容；1．分析设计任务，将其转化为一个最优化问题，建立数学模型：2．选用适当的最优化方法，利用电子计算机来求解数学模型，自动寻求最优方案。