机械零件的可靠性设计
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第734页(1553字)
在机械零件的强度计算中的各个量(载荷、面积、极限应力、弹性模量等)都不是确定量,而是服从于一定分布规律的在一定范围内取值的随机变量。如将一切引起失效的外部作用的参数称为应力,而把机械零件本身抵抗失效的能力称为强度,则应力-强度干涉模型就是进行机械零件概率设计的基本方法。
设机械零件应力随机变量为X,强度随机变量为Y,概率密度相应记为fs(x)、fr(y),其曲线如图3.3-3所示。若有重叠部分,则虽然工作应力的平均值μs值仍远小于极限应力(强度)的平均值μr,但不能保证工作应力在任何情况下都不大于极限应力,即工作应力大于零件强度的概率大于零,概率R=P(Y≥X)即为该机械零件的可靠度,其一般表达式为:
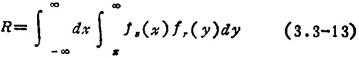
若已知应力和强度的分布密度,则可计算其可靠度。各常用分布的计算公式见表3.3-5,计算时,应使所求的R值不小于该零件的许用可靠度[R],即
R≥[R](3.3-14)
确定许用可靠度[R]值的主要依据是:零件的重要性、计算载荷的类别、载荷和应力等计算的精确程度、产品的经济性和社会影响因素。
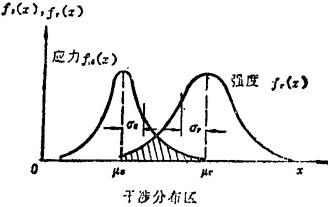
图3.3-3 强度-应力干涉模型
表3.3-5 强度与应力为各种常用分布时的可靠度计算公式

进行概率设计最重要的是取得数据,通过大量数据的统计处理以确定载荷(或应力)与强度的分布规律〔23〕(属表3.3-5中何种分布类型)及有关参数。试验表明,一些金属材料的强度特性基本为正态分布,表3.3-6为几种国产材料的强度数据。应该指出,由于生产条件和技术水平的差异,对于重要产品,且对强度要求很严时,应对材料直接进行试验,以统计得出所需的均值和标准差等数据。
表3.3-6 常用国产材料的强度数据 (MPa)
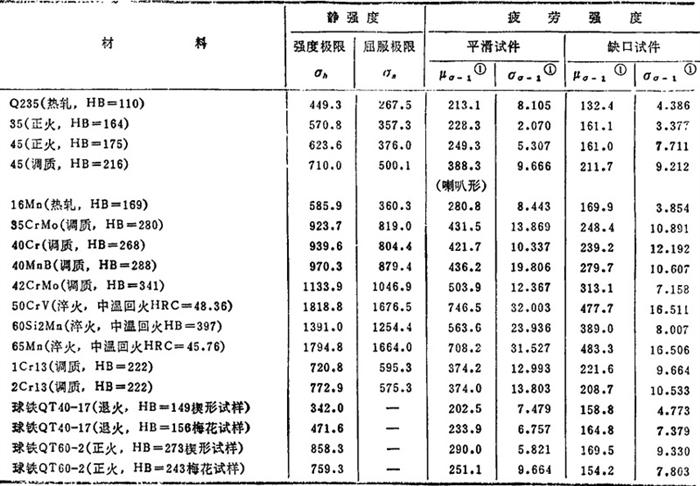
注:μσ-1为均值,σσ-1为均方差。
例3.3-4 一螺栓所受的工作应力服从正态分布,均值μs=350MPa,均方差(标准差)σs=28MPa;螺栓材料的强度也服从正态分布,其均值μr=420 MPa,均方差σr=28MPa,求可靠度,如设法控制强度的均方差,使降到σγ=14MPa,求可靠度。
解:如按常规设计,以强度和应力的均值来计算安全系数,得
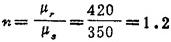
若按概率设计,由表3.3-5的公式
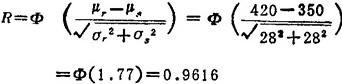
φ(1.77)的值系由表3.3-7按z=1.77查出。
若σγ降至14MPa,则
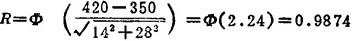
可见,当强度和应力的均值不变,缩小其中之一或二者的离散度,即可提高零件的可靠度。这一点,用常规的安全系数则无法反映。
表3.3-7 正态分布函数表
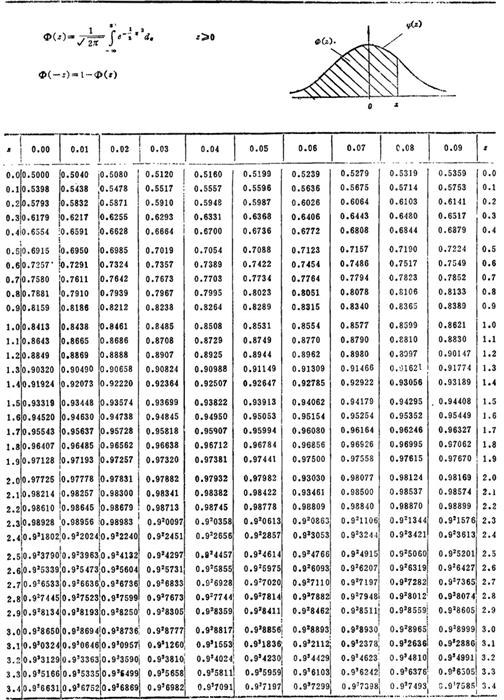
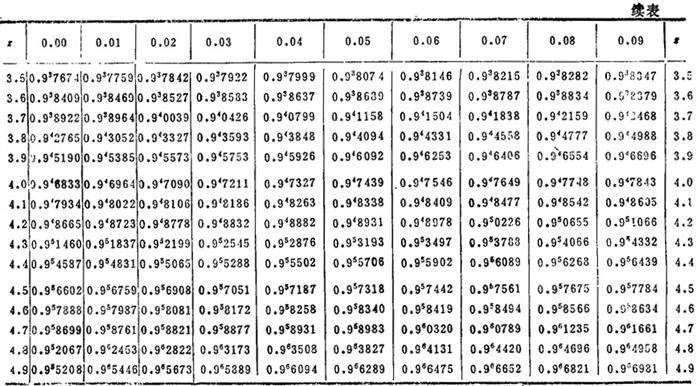
注:例如Φ(1.78)=0.96246,Φ(-2.42)=1-Φ(2.42)=1-0.99224=0.00776,Φ-1(0.99865)=3.0