函数的值域
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第15页(1770字)
1.函数值域的定义
在函数y=f(x)中,与自变量x的值对应的y的值叫做函数值,函数值的集合叫做函数的值域.
2.确定函数值域的原则
(1)当函数y=f(x)用表格给出时,函数的值域是指表格中实数y的集合;
(2)当函数y=f(x)用图象给出时,函数的值域指图象在y轴上的投影所覆盖的实数y的集合;
(3)当函数y=f(x)用解析式给出时,函数的值域由函数的定义域及其对应法则惟一确定.
3.求函数的值域的方法
(1)直接法——从自变量x的范围出发,推出y=f(x)的取值范围;
(2)分离常数法;
(3)配方法——利用换元法将函数转化为二次函数求值域(或最值);
(4)判别式法——运用方程思想,依据二次方程有实根,求出y的取值范围;
(5)换元法——适用于带有根式的函数;
(6)图象法——当一个函数图象可作时,通过图象可求其值域和最值;
(7)反解法.
例1 求函数值域
y=x2+2x+3,x∈[—1,2](配方法)
解 将二次函数配方有
y=(x+1)2+2,
由图象可知区间[—1,2]落在函数递增区间上.
由函数单调性可知
ymin=(—1+1)2+2=2,
ymax=(2+1)2+2=11.
∴函数值域为[2,11].
例2 求函数的值域

∴函数值域为{y|y≠1
注 形如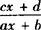 (a≠0)的函数值域可用此法.
(a≠0)的函数值域可用此法.
例4 求函数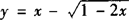 的值域.(换元法)
的值域.(换元法)
解 令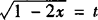 (t≥0)
(t≥0)
则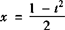
代入原函数
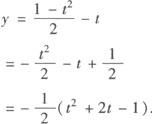
配方有
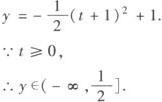
例5 求函数的值域(图象法)
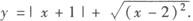
分析 解决此题的关键是去绝对值,采用零点分段法.
解 解法一(数形结合):画出函数的图象.
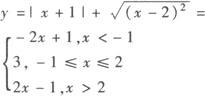
如下图所示,故值域y≥3.
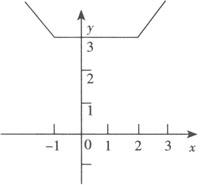
解法二(数形结合):
把y看作是点(x,0)到两定点A(—1,0)与B(2,0)的距离之和.故y≥|AB|=3.