对称问题
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第66页(2084字)
1.点关于直线对称问题
(1)点(a,b)关于点(x,y)的对称点坐标为(2x—a,2y—b).
(2)点(a,b)关于x轴,y轴,原点,直线y=x,直线y=—x的对称点分别为(a,—b),(—a,b),(—a,—b),(b,a)和(—b,—a).
(3)点A(x,y)关于直线x+y+c=0的对称点A′的坐标为(—y—c,—x—c).
(4)点A(x,y)关于直线x—y+c=0的对称点A′的坐标为(y—c,x+c).
(5)曲线f(x,y)=0关于直线x+y+c=0的对称曲线为f(—y—c,—x—c)=0.
(6)曲线f(x,y)=0关于直线x—y+c=0的对称曲线为f(y—c,x+c)=0.
2.若P,Q两点关于直线l成轴对称,则PQ的中点在直线l上且
kpO·k=—1(若PQ斜率存在)
3.曲线C∶f(x,y)=0与曲线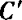 ∶g(x,y)=0关于点P(a,b)对称,则曲线C′上任一点M′(x,y),关于P的对称点M(2a—x,2b—y)在曲线C上,即
∶g(x,y)=0关于点P(a,b)对称,则曲线C′上任一点M′(x,y),关于P的对称点M(2a—x,2b—y)在曲线C上,即
g(x,y)=f(2a—x,2b—y).
4.曲线C:f(x,y)=0关于直线y=kx+b的对称曲线C′,则C′上任一点P关于直线y=kx+b对称的点必在曲线C上,即曲线关于直线的对称问题转化为点关于直线的对称问题.
例1 求点P(2,—1)关于点(3,4)的对称点坐标.
分析 利用中点坐标公式.
解 设对称点P′(x,y),
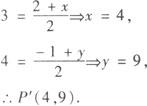
点评 将点关于点对称问题转化为线段中点问题
例2 求点A(2,2)关于直线l∶2x—4y+9=0的对称点的坐标.
分析 两点A、B关于直线l对称,即为AB⊥l,垂足M为线段AB中点.
解 设对称点B(a,b)
∵直线l的斜率存在且不为0,
∴直线AB的斜率存在,

将①②联立解得:a=1,b=4,
∴对称点B(1,4).
例3 已知直线l∶3x—y+3=0.
求:(Ⅰ)直线l关于点P(4,5)的对称线;
(Ⅱ)直线x—y—2=0关于直线l的对称直线方程.
解 (Ⅰ)在直线l∶3x—y+3=0上取两点:
A(—1,0),B(0,3),
则A、B两点关于点P(4,5)的对称点为A′(9,10),B′(8,7).
由两点式过A′,B′的直线为
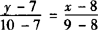
即 3x—y—17=0.
(Ⅱ)联立两直线方程得
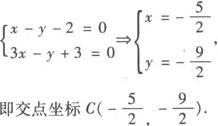
又∵直线x—y—2=0的斜率k1=1,
直线l的斜率k2=3.
设所求对称直线斜率为k,
由到角公式有:
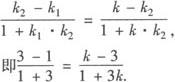
解得k=—7由点斜式所求对称直线的方程为y+9/2=—7(x+5/2),
即7x+y+22=0.