直线与抛物线
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第83页(1653字)
例1 已知抛物线y2=—8x,过点P0(—1,1)引一条弦,使此弦在P0点被平分,求弦所在的直线方程.
解 设所求弦的直线方程为
y—1=k(x+1),
即y=kx+k+1
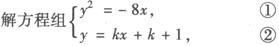
把①代入②得
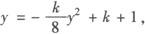
即ky2+8y—8k—8=0.
设所求弦的两端点为(x1,y1),(x2,y2)由韦达定理,得
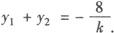
又∵P0(—1,1)是弦的中点,
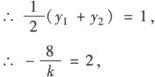
即k=—4.
∴此弦所在直线方程为:
4x+y+3=0,
例2 A、B是抛物线y2=2px(p>0)上的两点,且OA⊥OB(O为坐标原点),求证:
(1)A、B两点的横坐标之积,纵坐标之积分别都是定值;
(2)直线AB经过一个定点.
证明 (1)设A(x1,y1),B(x2,y2),则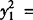
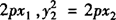 .
.
因为OA⊥OB,所以x1x2+y1y2=0,
所以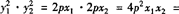 —4p2y1y2,
—4p2y1y2,
所以y1y2=—4p2为定值,x1x2=—y1y2=4p2也为定值.
(2)因为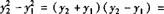 2p(x2—x1),
2p(x2—x1),
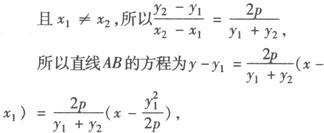
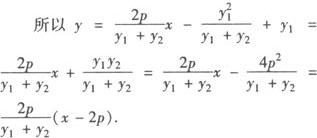
所以直线AB过定点(2p,0).
例3 抛物线C的顶点在原点,焦点在x轴正半轴上,若点A(—1,0)和点B(0,8)关于过圆点O的直线l的对称点都在C上,求直线l和抛物线C的方程.
策略 本题可用待定系数法,设出直线l和抛物线C的方程,再求出点A和B关于l的对称点A′和B′,根据A′、B′的坐标(含参数)满足抛物线方程得出关于两个参数的方程组,解出参数值即可求出l和C的方程.
解 由题意设直线l和抛物线C的方程分别为y=kx(k≠0)和y2=2px(p>0).
设A(—1,0)和B(0,8)关于l的对称点分别为A′(x1,y1),B′(x2,y2),

∵A′、B′在抛物线C上.
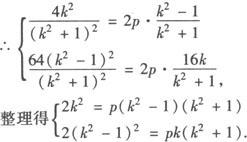
①÷②消去p,整理得k=k2—1,
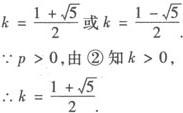
把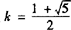 代入①得
代入①得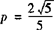 .
.
所以,直线l的方程为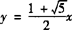 ,抛物线C的方程为
,抛物线C的方程为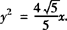 .
.