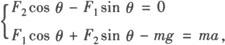超重和失重

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第180页（2174字）

(1)超重现象：物体对支持物的压力(或对悬挂物的拉力)大于物体所受重力的情况称为超重现象．

物体具有向上的加速度(包括向上加速运动和向下减速运动)时，物体对水平支持面的压力或对竖直悬挂物的拉力大于本身重力的现象，也称为“视重”大于实重现象．

(2)失重现象：物体对支持物的压力(或对悬挂物的拉力)小于物体所受重力的情况称为失重现象．

物体具有向下的加速度(包括向下加速运动和向上减速运动)时，物体对水平支持面的压力或对竖直悬挂物的拉力小于本身重力的现象，也称为“视重”小于实重现象．

(3)完全失重现象：当物体向下的加速度等于重力加速度时，物体对水平支持面的压力或对竖直悬挂物的拉力为零的现象，也称为“视重”等于零的现象．

不论超重、失重或完全失重，物体的重力依然不变，只是“视重”改变，重力是由于地球对物体的吸引而产生的，地球对物体的引力不会由于物体具有向上或向下的加速度而改变．

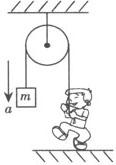
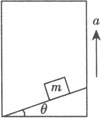
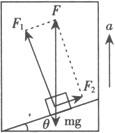
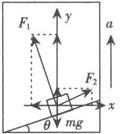
例1 质量为M的人站在地面上，用绳通过定滑轮将质量为m的重物从高处放下，如图所示，若重物以加速度a向下降(a

A．(m+M)g—ma

B．M(g—a)—ma

C．(M—m)g+ma

D．Mg—mg

分析 用隔离法分别研究重物m和人的受力情况及运动情况，应用牛顿第二定律列式求解，注意重物处于失重状态，人处于平衡状态．

以重物m为研究对象，物体受重力mg，方向竖直向下；绳的拉力T，方向竖直向上两个力的作用，取加速度a的方向为正方向，由牛顿第二定律，有mg—T=ma

T=m(g—a)

研究人：人受重力Mg，地面支持力N，绳的拉力T三个力作用，处于平衡状态，故有N+T—Mg=0．

将T的表达式代入上式，解得N=(Mm)g+ma．

由牛顿第三定律可知，人对地面的压力大小为N′=N=(M—m)g+ma．

答 C．

例2 如右图所示，一质量为m的物块放在升降机中的斜面上，斜面倾角为θ．当升降机以竖直方向的加速度a匀加速上升时，物体相对斜面静止，则斜面对物体的支持力和摩擦力各是多大?

分析一 运动分析入手，结合受力分析，根据牛顿第二定律列方程求解．

以物块m为研究对象，进行受力分析，物块受重力mg、斜面对它的支持力F₁，斜面对它的静摩擦力F₂三个力作用，各力方向如右图所示，因物块相对斜面静止，具有与升降机相同的加速度a，故F₁和F₂的合力必竖直向上，利用平行四边形定则求出F₁和F₂的合力F，再根据牛顿第二定律，有F—mg=ma． ①

根据平行四边形定则，有F₁=Fcosθ，②

F₂=F·sinθ． ③

由以上三式解得：F₁=m(a+g)cosθ

F₂=m(a+g)sinθ．

分析二 m的受力情况和运动情况，建立直角坐标系，如右图所示，用正交分解法求解．

解 将F₁和F₂沿着x轴和y轴方向分解．

F_1x=—F₁sinθ，F_1y=F₁cosθ；

F_2x=F₂cosθ，F_2y=F₂sinθ；

根据牛顿第二定律列出分量式方程：

联立求解①、②两式

联立求解①、②两式，得F₁=m(a+g)cosθ，F₂=m(a+g)sinθ．