简谐运动图象的物理意义
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第228页(1679字)
1.图象描述了做简谐运动的质点的位移随时间变化的规律,即是位移一时间函数图象.切不可将振动图象误解为物体的运动轨迹.
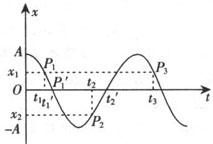
2.图象的用途 如图表示一质点做简谐运动的图象,从图中可以知道:
(1)任一时刻质点的位移,例如,在t=0时x=A,即质点在t=0位移是正向最大;在t=t1时,图线上的对应点为P1其纵坐标为—x1,则表示t1时刻质点的位移x1.
(2)振幅A.
(3)周期T:过P1作t轴的平行线,交曲线上的点P3(t3、x1),则周期T=t3—t1.
(4)速度方向:由图线随时间的延伸就可以直接看出,譬如,t1时刻质点的位移为x1,图线向下质点回到了平衡位置,t2时刻质点的位移为x2,此时图线是向上延伸的,可知质点是向x轴正方向运动的,t2′时刻质点回到了平衡位置.
(5)加速度:由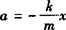 ,知加速度与位移的大小成正比,而方向总与位移方向相反,只要从振动图象中认清位移(大小和方向)随时间变化的规律,加速度随时间变化的情况就迎刃而解了,如在t0到t1的过程中,a为负向,x减小则a随之减少.
,知加速度与位移的大小成正比,而方向总与位移方向相反,只要从振动图象中认清位移(大小和方向)随时间变化的规律,加速度随时间变化的情况就迎刃而解了,如在t0到t1的过程中,a为负向,x减小则a随之减少.
3.关于振动图象的讨论 简谐运动的图象不是振动质点的轨迹,做简谐运动质点的轨迹是质点往复运动的那一段线段(如弹簧振子)或那一段圆弧(如下一节的单摆).这种往复运动的位移图象,就是以x轴上纵坐标的数值表示质点对平衡位置的位移,以t轴横坐标数值表示各个时刻,这样在x—t坐标系内,可以找到各个时刻对应质点位移坐标的点,即位移随时间分布的情况——振动图象,例如在上图中P1的坐标表示为(t1,x1)并不表示t1时刻质点在P1点,而是表示在t1时刻质点离开平衡位置在正方向上的位移是x1,所以振动图象并不是质点的运动轨迹.
简谐运动的周期性,体现在振动图象上是曲线的重复性.
简谐运动是一种复杂的非匀速运动,但运动的特点具有简单的周期性、重复性、对称性,所以用图象研究要比方程直观、简便.简谐运动的图象随时间的增加逐渐延伸,过去时刻的图象形状将永远不变.任一时刻图象上过该点切线的斜率数值代表该时刻振子的速度大小,正负表示速度的方向,正时沿x正向,负时沿x负向.
例 如图所示,是水平方向甲、乙两个弹簧振子的振动现象,由图象可知( ).

A.两弹簧振子完全相同
B.两弹簧振子所受回复力的大小之比F甲∶F乙=2∶1
C.振子甲速度为零时,振子乙速度一定最大
D.振子振动频率之比f甲∶f乙=1∶2
分析 两振子的周期从图象上可看出不相同,且知T甲∶T乙=2∶1,故f甲∶f乙=1∶2,D项正确,而振子的周期是由振动本身即弹簧的劲度k和振子的质量m的确定的,周期不同则振子不完全相同,A项错误,而最大回复力F=—kA,由于k不一定相同,故F就不一定与x成正比,故B项错,从图象上可以看出,甲在第一个周期内速度为零时,乙的速度最大,因图象的周期性反映振动的周期性,故在以后的振动中都会出现甲速度为零(在最大位移处)时,乙速度最大,故C项正确.
答 C、D.