特殊点的坐标特征

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第49页（2956字）

1．象限点：第一象限点：横、纵坐标均为正，即(+，+)．

第二象限点：横坐标为负，纵坐标为正，即(－，+)．

第三象限点：横、纵坐标均为负，即(－，－)．

第四象限点：横坐标为正，纵坐标为负(+，－)．

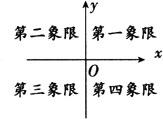
注意 记忆方法：一全正，二纵正，三无正，四横正．

2．坐标轴上的点：

横轴上的点的纵坐标为0，纵轴上的点的横坐标为0，原点横、纵坐标均为0．

即：横轴上的点的坐标，可以记作(x，0)．

纵轴上的点的坐标，可以记作(0，y)．

原点坐标记作(0，0)．

3．平行于坐标轴的直线上的点：

平行于x轴的直线上的所有点的纵坐标相同；

平行于y轴的直线上的所有点的横坐标相同．

4．对称点：

关于x轴对称的两点，横坐标相同，纵坐标互为相反数；

关于y轴对称的两点，纵坐标相同，横坐标互为相反数；

关于原点对称的两点，横、纵坐标均互为相反数．

即：点P(x，y)关于x轴的对称点P₁的坐标(x，－y)；

点P(x，y)关于y轴的对称点P₂的坐标(－x，y)；

点P(x，y)关于原点的对称点P₃的坐标(－x，－y)．

5．象限角平分线上的点：

第一、第三象限两坐标轴夹角平分线上的点的横坐标、纵坐标相等；

第二、第四象限两坐标轴夹角平分线上的点的横坐标、纵坐标互为相反数．

例1 下列各点，在第三象限的是( )．

A．(2，4) B．(2，－4)

C．(－2，4) D．(－2，－4)

答 D．

[解析] 第三象限点的横、纵坐标均为负．

例2 下列说法错误的是( )．

A．如果一点的横坐标、纵坐标都为0，那么这个点是原点

B．纵轴上的点的横坐标为0

C．如果一点的横坐标为0，那么这个点必在横轴上

D．如果一点的纵坐标为0，那么这个点必在横轴上

答 C．

[解析] 横轴上点的纵坐标为0；纵轴上点的横坐标为0．

例3 如果点A(a，b)在第四象限，那么点(－a，－b)在( )．

A．第一象限 B．第二象限

C．第三象限 D．第四象限

答 B．

[解析] ∵A(a，b)在第四象限，

∴a>0，b<0．

∴－a<0，－b>0．

∴(－a，－b)在第二象限．

例4 已知点P(a+3，7+a)位于二、四象限的角平分线上，则a=＿＿．

答 －5．

[解析] 第二、四象限角平分线上的点的横、纵坐标互为相反数．

故a+3+7+a=0．

所以a=－5．

例5 已知点A(m，n)，它关于原点对称的点是A₁，而A₁关于x轴对称的点是A₂，且点A₂的坐标是(－3，2)，求m，n的值．

解 ∵点A的坐标(m，n)．∴点A关于原点的对称点A₁的坐标(－m，－n)．∴A₁关于x轴对称的点A₂的坐标为(－m，n)，而点A₂的坐标是(－3，2)，则有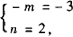即m=3，n=2．

[解析] 注意对称点的坐标特征．

例6．点P(m，1)在第二象限内，Q点(－m，0)在( )．

A．x轴正半轴上 B．x轴负半轴上

C．y轴正半轴上 D．y轴负半轴上

答 A．

[解析] ∵P在第二象限内∴m<0∴－m>0．

又∵Q点纵坐标为0．∴必在横轴上，故选A．

例7 过(1，－3)且平行于y轴的直线上的点( )．

A．横坐标都是1

B．纵坐标都是－3

C．横坐标都是－3

D．纵坐标都是1

答 A．

[解析] 平行x轴的直线上的点的纵坐标相同．

平行y轴的直线上的点的横坐标相同．