反比例函数关系中的定值问题

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第65页（1583字）

在反比例函数y=k/x(k≠0)的图象上任取一点，过这一点分别作x轴、y轴的平行线，与坐标轴围成的矩形面积总等于常量|k|．

例1 已知反比例函数y=－5/x(x<0)的图象上任取一点P，过P分别作x轴、y轴的垂线，垂足分别为A、B，那么四过形AOBP的面积为＿＿．

答 5．

[解析] 根据四边形AOBP的面积=PA·PB=|xy|=|－5|=5．

例2 反比例函数图象如图所示，P是其图象上的一点，P点到两个坐标轴的垂线段与坐标轴围成的矩形面积为6，则此函数的解析式为：＿＿．

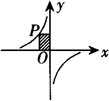
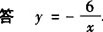
[解析] ∵矩形面积为6，

∴|xy|=6=|k|，

∴k=±6．

∵图象在第二、四象限，

例3 如图，P是反比例函数y=4/x在第一象限分支上的一动点，PA⊥x轴，随着x逐渐增大，△APO的面积将( )．

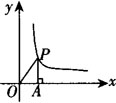
A．增大 B．减小

C．不变 D．无法确定

答 C

[解析] ∵S_△APO=1/2·|xy|=1/2|k|=1/2×4=2．

∴随着x逐渐增大，△APO的面积保持不变．

例4 如图，点A在反比例函数y=k/x的图象上，AB垂直于x轴，若S_△AOB=4，那么这个反比例函数的表达式为＿＿．

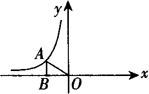
[解析] ∵S_△AOB=1/2·|x·y|=1/2|k|=4．

∴|k|=8．∴k=±8．

又∵图象在第二象限，

∴k=－8，∴y=－8/x．

例5 如图，直角三角形AOB的顶点A是直线y=－x－0．3m与双曲线y=m/x在第二象限的交点，且S_△AOB=5求

(1)m的值；(2)△ABC的面积．

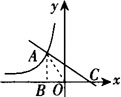
解 (1)设A点坐标为(x，y)，则S_△AOB=1/2|x||y|=5．

∵A在第二象限，

∴xy=－10，即m=－10．

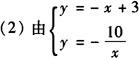
解得A点坐标为(－2，5)又C点坐标为(3，0)．

∴S_△ABC=1/2|AB||BC|=1/2×5×5=12．5．