角平分线

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第87页（2305字）

从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线．

注意 角平分线的定义暗含三个关系．

若OC是∠AOB的平分线，则有：

1．∠AOC=∠BOC(等量关系)．

2．∠AOB=2∠AOC，∠AOB=2∠BOC(2倍关系)．

3．∠AOC=1/2∠AOB，∠BOC=1/2∠AOB(一半关系)．

例1 在同一平面内，下面叙述中，能够表示是∠AOB的平分线的是( )．

A．∠AOC=∠BOC

B．∠AOC=1/2∠AOB

C．∠AOB=∠BOC

D．∠AOC+∠BOC=∠AOB

答 A．

[解析] B选项中射线OC可能在∠AOB的外部．

C选项中表示射线OB是∠AOC的角平分线．

D选项中仅能说明射线OC是∠AOB内部一条射线．故选A．

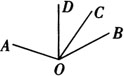
例2 下图中的∠AOB为一钝角，OC、OD是两条射线，且OD平分∠AOB，若∠AOC=α，∠BOC=β(α>β)，试用关于α、β的代数式表示∠COD的大小．

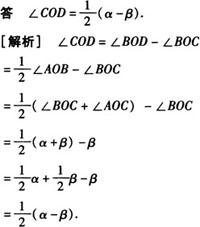
例3 已知A、O、B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC，①量出图中∠DOE的度数；②若∠AOC=40°，求∠DOE的度数；③若∠AOC=60°，求∠DOE的度数；④∠DOE的度数是否是固定的?如果是，度数是多少?如果不是，说明理由．

答 ①90°；

②90°；

③90°；

④是，90°．

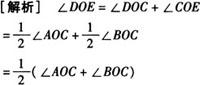
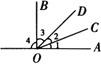
例4 如图，OC为∠AOD的角平分线，∠4=90°，且∠2∶∠3∶∠4=1∶2∶4，求∠1的度数．

答 22．5°．

[解析] ∵∠4=90°，

∠2∶∠3∶∠4=1∶2∶4，

∴∠2=22．5°，∠3=45°．

∵OC平分∠AOD，

∴∠1=22．5°．

例5 如图所示，已知：∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC．

①求∠MON的度数．

②如果①中∠AOB=α其他条件不变求∠MON的度数．

③如果①中∠BOC=β(β为锐角)其他条件不变，求∠MON的度数．

④从①②③中的结果能看出什么规律?

答 ①∠AOC=∠AOB+∠BOC=90°+30°=120°，

∵OM平分∠AOC，

∴∠MOC=60°．

又∵ON平分∠BOC，

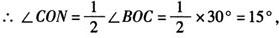
∵∠MON=∠MOC－∠CON=60°－15°=45°．

②∠AOC=∠AOB+∠BOC=α+30°，

∵OM平分∠AOC，

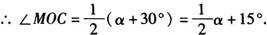
又∵ON平分∠BOC，

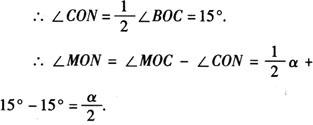
③同理：∠MON=45°．

④∠MON的度数是∠AOB度数的一半，与∠BOC的度数无关．