相似多边形的性质

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第138页（835字）

1．相似多边形的对应角相等，对应边成比例．

2．相似多边形周长的比等于相似比．

3．相似多边形面积的比等于相似比的平方．

例1 如图，在矩形ABCD中，E、F分别在BC、AD上，矩形ABCD相似于矩形ECDF，且S_矩形ABCD=3S_矩形ECDF，AB=2，求S_矩形ABCD．

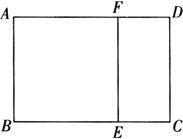
解 因矩形ABCD相似于矩形ECDF，且S_矩形ABCD=3S_矩形ECDF，

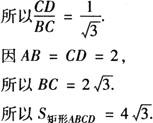
例2 如图，已知△ABC中，DE∥BC，S_△ADE∶S_{四边形BCED}=1∶2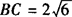，，试求DE的长．

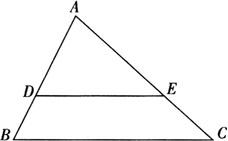
解 因为DE∥BC，

所以∠ADE=∠B，

又∠A=∠A，

所以△ADE∽△ABC．

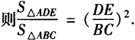
又S_△ADE∶S_{四边形BCED}=1∶2，

设S_△ADE=a，则S_{四边形BCED}=2a

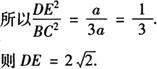
[解析] 此题综合应用相似三角形的判定，相似三角形面积比等于相似比的平方这一性质，求得边长．需要注意的是，所给的是三角形与四边形的面积比，必须转化成两个相似三角形的面积比．