绘制频数分布直方图的一般步骤

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第192页（1466字）

1．计算最大值与最小值的差(极差)，确定统计量的范围．

2．决定组数和组距．数据越多，分的组数也应越多，当数据在100个以内时，通常按数据的多少分成5～12组．组距是指每个小组的两个端点之间的距离，实践中通常要求各组的组距相等．

3．确定分点：为了保持组距相等，往往把最小值减小一点作为最左边的分点；把最大值加大一点作为最右边的分点．

4．列频数分布表：列表时可采用数票法进行累计．

5．画频数分布直方图．

注意 当收集的数据连续取值时，绘制的就是反映连续型统计量的频数分布直方图．那么各个“条形”之间就应该是连续的，而不应该有间隔；当各组的组距相等时，所画的各个“条形”的宽度也应相同．

例1 对36个人的身高量出一组数据，如果取组距为5cm，那么可将数据分成6组，看表填空：

(1)第三组和第五组频数分别是＿＿和＿＿．

(2)数据中的最大值是＿＿，最小值是＿＿，它们的差是＿＿．

(3)第一组和第四组频率分别是＿＿和＿＿．(精确到0．01)

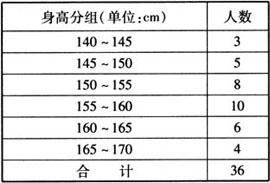
答 (1)8，6．

(2)170，140，30．

(3)0．08，0．28．

例2 为了解学生的体能情况，抽取了某学校一个年级的部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频数分布直方图，如图所示，已知图中从左到右前三个小组的频率分别为0．1，0．3，0．4，第一小组频数为5．

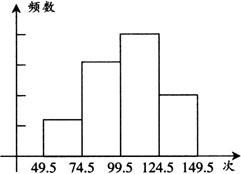
(1)求第四小组的频率?

(2)参加这次测试的学生数是多少?

(3)若次数在75次以上(含75次)为达标，试估计该年级学生跳绳测试的达标率是多少?

解 (1)∵各小组频率之和为1，

∴第四小组的频率为1－(0．1+0．3+0．4)=0．2．

(2)∵第一小组的频率为0．1，频数为5．

∴参加这次跳绳的学生数为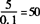(人)．

(3)跳绳测试的达标率为．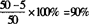

[解析] 频数分布直方图通过等宽的小矩形的高表示各组相应的频数，每一个小矩形的高代表各组相应的频数，所以频数越多，矩形就越高，频数的多少可根据左边对应的数量确定，因此频数分布直方图能形象直观的反映各组频数的多少，是统计中表示量的常见的形式．