比较静态分析

出处：按学科分类—政治、法律 经济科学出版社《政治经济学大辞典》第279页（3416字）

又称为比较静态学。

它是通过比较一个系统变化前后两个不同的均衡位置来分析模型参数变动所产生的影响的一种方法。或者说它是“研究经济变量对其所依存环境的变化是如何作出反应的”(H．Varian，1992，P．31)。“比较(comparative)”一词，是指要比较变化前后的两种状态，“静态(statics)”一词反应了这样一种思路：比较是在所有调整完成以后进行的，即我们只比较两个均衡状态。这也同时表明了这种方法的局限性所在：“它没有分析导致初始均衡状态的历史动力，也没有分析从一种均衡状态调整到另一种均衡状态的转换过程”(约翰·伊特韦尔、默里·米尔盖特、毕得·纽曼，1996，P．562)。

比较静态分析这个术语看起来仅在经济学中使用，在许多其他研究领域，这种分析方法一般称之为灵敏度分析(sensitivity analysis)，不过这个术语在经济学中已经根深蒂固，它的历史几乎和经济学一样古老。

这种分析方法渗透于经济学的各种均衡分析中，新古典学派的经济学家尤其喜欢采用这种方法。

希克斯(Hicks，1939)首先用公式表示了新古典学派的比较静态分析方法，保罗·萨缪尔森(1983)将它抽象为一种一般化的方法，使其条理更加清楚。“从体系有解，函数可微，偏导数矩阵可逆的假定出发，由逆函数定理推导出体系隐含均衡条件的局部惟一解，又在一定的假设下由隐函数定理推出参数表示的连续解函数的存在，再通过解函数对参数微分，由连锁法则推出比较静态乘子，从而不但描述了静态分析——只关心在什么地方(特定结构中)达到均衡，而不问能否、怎样和何时达到均衡——的一般结构，而且揭示了比较静态和静态分析的内在关系，精确地给出了比较静态分析的一般公式。”(费方域，1992，P．11)。

保罗·萨缪尔森(1983)加以一般化的这种方法表述如下：

给定m个由经济环境决定的参数(a₁，a₂，……，a_m)，它们是模型的外生变量，可以包括像货币供给和税率这样的政府政策变量，也可以是反映气候状况或消费者偏好的参数；再给定n个规定经济制度状况的变量或者说未知数(x₁，x₂，……，x_n)(n可以大于也可以小于m)，它们是模型的内生变量，新古典学派的均衡分析中最有代表性的内生变量是商品价格。但这并不是说在所有模型中价格都是内生变量，这要视情况而定，如在利润函数或成本函数中一般把产品和要素价格作为既定的外生变量，而把产品供给和要素需求视为内生变量。假设存在n个包含这些变量及参数的独立且相容的函数关系式。

最一般的它们可以用隐含的形式写出来。每个方程都包含所有的变量和参数。其形式如下：

f¹(x₁，……，x_n；a₁，……，a_m)=0

f²(x₁，……，x_n；a₁，……，a_m)=0

… … … (1)

fⁱ(x₁，……，x_n；a₁，……，a_m)=0

… … …

fⁿ(x₁，……，x_n；a₁，……，a_m)=0，

或者更简洁地写为：

fⁱ(x₁，……，x_n；a₁，……，a_m)=0

i=1，2，……，n

也可以写成向量形式：

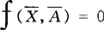
其中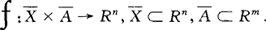

这些方程本身就是均衡条件。需要特别注意的是内生变量的数目必须与均衡条件的数目相等。

如果方程满足以下三个假设，那么相应于任何一组预先给定的参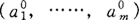可以认为它们能够确定出未知数的一组惟一的值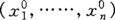这三个假设是：

(1)方程组有解。

(2)fⁱ(i=1，2，……，n)是连续可微的。

(3)n×n阶偏导矩阵：

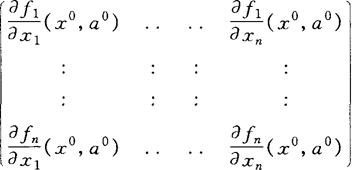
是可逆的，其中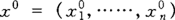，a⁰=。

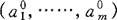在这样的假设下，微积分学的逆函数定理告诉我们：在x⁰的一个微小领域中，x⁰=f^－1(0，a⁰)是均衡条件的局部惟一解。而隐函数定理告诉我们：存在着以下连续函数：

x_i=gⁱ(a₁，……，a_m)，i=1，2，……，n (2)

满足：fⁱ(g¹(a₁，……，a_m)，……，gⁿ(a₁，……，a_m)；a₁，……，a_m)=0，i=1，2，……，n

从均衡方程中可以计算出未知数相对于任何参数的变化率，也就是说参数的微小变化对未知数的影响，我们以相对于a₁的变化率为例，作为一种记号，令：

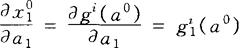
表示当所有的其他参数保持不变时，第i个变量相对于参数a₁的变化率，也就是a₁的微小变化对x₁的影响。

必须在参数一组给定的值上及未知数一组对应的值上计算这些偏导数，考虑初始位置：

以及相对应的一组未知数值：

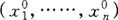
我们有：

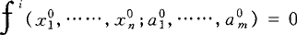
i=1，2，……，n (3)

而且：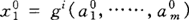

i=1，2，……，n (4)

这是因为未知数必须满足均衡条件，利用连锁法则对(1)式的每个方程关于a₁进行微分，记住所有的其他参数保持不变，但所有的未知数都是变量，我们得到：

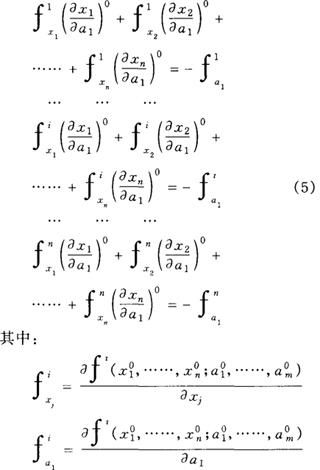
i，j=1，2，……，n

在所讨论的均衡点上这些偏导数的值是确定的。

方程(5)实际上就是一个具有n个未知常系数线性方程组，这个方程组的解依赖于其系数的值。

上面的假设(3)已经保证了方程组(5)的系数矩阵是可逆的，所以可以得出：

未知数相对于其他参数a_i(i=2，……，n)的变化率以相同的方法求出。

这样就可以得到一个n×m阶的矩阵：

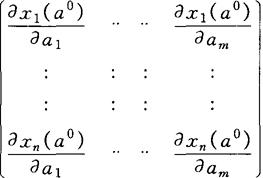
其中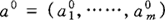这个矩阵中的元素被称之为比较静态乘子(萨缪尔森，1983)，或译为比较静态学乘数。例如，当第一个参数由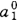a变为a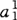时，如果]足够小，则内生变量x₁的值就由x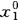近似地变成：

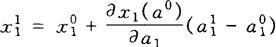
比较静态分析方法在新古典学派的均衡分析中得到了广泛的应用，但从20世纪50年代开始，注意的重点从推导模型的比较静态特征转向说明均衡的存在性，这一点对于比较静态分析是至关重要的，稳定的均衡解的存在是应用比较静态分析的基础。

参考文献：

约翰·伊特韦尔等编，1996，《新帕尔格雷夫经济学大辞典》，第1卷，经济科学出版社。

费方域，1992，《新古典经济学的古典数学总结(译序)》《经济分析基础》，保罗·萨缪尔森，商务印书馆。

厉以宁、秦宛顺，1992，《现代西方经济学概论》，北京大学出版社。

希克斯，1939，《价值与资本》，商务印书馆。

H．Varian，1992，Microeconomic Analysis，W．W．Norton Company，Inc．