贝叶斯游戏
出处：按学科分类—政治、法律 经济科学出版社《政治经济学大辞典》第803页（2533字）
又称贝叶斯博弈。
该理论研究在不完全信息条件下，人们将在没有确定了解也不了解客观概率时对相关客体做出的主观概率判断，这种判断可以用期望效用最大化来进行刻划求解。
博弈论于1944年由美国的冯·纽曼(Neumann)和摩根斯顿(Morgenstern)创立。
最初理论研究的博弈结构只有三个部分：一是参加者，假设所有参加博弈的人都是理性的；二是策略空间，参加者必须知道自己及其他人的策略选择范围，以及各种策略间可能的因果关系。三是评价结果，可以用数值表示各个参加者在各种可能结果下获得的收益或亏损，这种数值叫“支付”。这三个部分构成博弈规则。但是人们很快意识到这种博弈结构需要深化，在实际过程中，参加博弈的人对其他人并不完全了解，比如无法确切地知道他们的决策能力、主观偏好和自然秉赋等等，所有这些不完全信息都可归结为对支付的不完全了解。
1968年德国的豪尔绍尼(Harsanyi)从理论上回答了不完全信息博弈问题的求解问题，他引进特征和概率两个部分，扩展了原先的博弈结构。所谓特征，又称类型，是指与参加者决策有关的私有信息总和。这样参加者知道自己的实际特征，但不知道其他参加者的实际特征。但是所有参加者都知道关于可能特征的公共信息，即参加者可能特征上的一种联合概率分布。
参加者只能对其他参加者的实际特征作出主观概率判断，然后根据这种主观概率进行选择。这就需要应用贝叶斯理性原则：人们将在没有确定性了解也不了解客观概率时对相关客体做出主观概率判断，并据之进行决策。
在满足一定技术性条件时，人们的理性行为能由期望效用最大化来进行描述。因此这种解法被称为贝叶斯博弈理论。
用数学形式来表述贝叶斯博弈理论：设集合T=(N，T，C，P，U)，其中N是参加者构成的集合，N=｛1，2，……，n｝。T是特征集，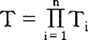
i。Ti是参加者i的特征集，
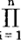表示笛卡儿积。C是策略空间
i。Ci是参加者i的策略空间。P是特征概率分布函数向量。
P=(P1，P2，……，Pn)。Pi是参加者i对其他参加者特征分布的主观概率。定义～i为除i外所有其他参加者的集合，即－i=｛j∶j=1……，n以及j≠i｝。定义T－i为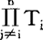
i。
由于贝叶斯博弈假定各参加者知道自己的特征，用ti来代表集合Ti中的元素——即i的真实特征，用t－i来代表集合T－i中的任一元素，参加者i对其他参加者特征的分布可由一简化的主观条件概率函数来代表：pi(t－i／ti)，其中ti为参加者i所知道。显而易见，
∫ti∈T－iPi(t－i｜ti)dt－i=1
U是效用函数向量。U=(u，，u2，……，un)。U概括了所有可能游戏结果下的各人所获支付。
ui是参加者i的效用系数。它是单维数值，取决于策略组合及参加者的真实特征。也就是Ui：C×T→R。
从参加者i的角度上看，如果所有其他参加者～i选定的策略组合是c－i，要力图扩大他自己的期望支付，他的准则是找到一个具体的最佳战略ci*，满足于
Ci*=argmax∫t－i∈T－iui(ci，c－i，ti，t－i)·pi(t－ilti)dt-i
纳什均衡点是一个c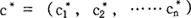
)，在这个c*上，每个参加者主观上都采取最佳战略手段。简言之，纳什均衡点是一个共同解
，满足于这样一个方程组：
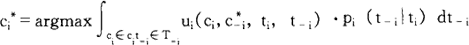
(i=1，2，……，n)
在贝叶斯博弈中求解纳什均衡点，由于运用贝叶斯理性原则和推断方法而称为贝叶斯均衡。
贝叶斯均衡点可能不存在，也可能有多个，而且其中有一些可能是不合理的。为了排除这些不合理均衡，完善贝叶斯均衡，后来相继提出了序列均衡、颤抖手完美均衡和适当均衡等概念，但是直到现在，仍然没有那一种解的概念能保证博弈仅存在惟一的“理性”均衡。
贝叶斯博弈理论在博弈论体系中占据重要地位，它被用来重新解释博弈论的基本概念和分析方法。
其中最重要的是混成策略概念的重新解释。现实博弈局势总要受一些微小的随机干扰因素影响，这些干扰的具体值只为参加者自己知道，不为其他人了解，所以应该建模为不完全信息博弈。可以证明，这些具有微小扰动的不完全信息博弈在原混成策略的均衡点附近总具有惟一的纯策略贝叶斯均衡点，而且当这些微小扰动强度超于零时，贝叶斯均衡点会趋向于原混成策略均衡点。
1994年，豪尔绍尼与纳什(Nash)和塞尔腾(Selten)因为对博弈论的杰出贡献而获得诺贝尔经济学奖。
参考文献：
Harsanyi，J．C．，1967—1968，Game with incomplete information played by Bayesian players．Management Science Vol．14，159—82．320—34．486—502．
Harsanyi，J．C．，1973：“ames with randomly distributed pay off a new rationale for mixed strategy equilibrium points”ternational Journal of Game Theory Vol．2，1—23．
汤敏、茅于轼主编，1989，《现代经济学前沿专题》第一集，商务印书馆。