假设检验

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第91页（1062字）

判断在样本所提供的信息与关于总体分布的某种假设之间是否存在显着差异的手续，叫做假设检验。

对于总体分布的假设称作零假设。通常记作H₀。除零假设外，还要同时考虑另一个对立的假设，称作对立假设，记作H₁。例如，已知一车间加工的某种零件的尺寸服从正态分布N(μ，σ²)，其中μ是尺寸均值，σ²是方差。

按加工规格的要求应有μ=μ₀，μ₀是个已知常数。如果要检验某批产品是否合乎规格，就可以提出零假设H₀：μ=μ₀，其对立假设可以根据实际需要有所不同。

可以是H₁：μ=μ₀，或者如果所担心的问题仅是尺寸过小，对立假设就可以是H₁：μ＜μ₀。

假设检验要通过某种手续接受H₀或拒绝H₀，检验手续的基本步骤是：构造一个适当的统计量，该统计量应该反映样本对于零假设H₀所提供的信息，至少当H₀成立时，该统计量的分布是已知的。

从分布可以看出统计量的值落在什么范围内的概率应该是很小的，也就是，如果H₀成立，那么统计量的值就不太可能落在这个范围内。

这种情形发生时就拒绝H₀。

这样做的结果可能出现两种错误，一是H₀真，但我们拒绝了H₀，这称做第一类错误。二是H₀不真，但是我们接受了H₀，称做第二类错误。

要使犯两类错误的概率同时减小是做不到的，通常的做法是把犯第一类错误的概率限制在一个很小的水平α上，如α=0．01、，0．05、0．1，然后使犯第二类错误的概率尽可能地小。常数α称作检验水平。

例如，考虑前面提到的检验一批产品是否合乎规格的问题。

设任意抽出n个产品测量其尺寸，得数据X₁……，X_n。提出零假设H₀：μ=μ₀，对立假设μ≠μ₀。取置信水平为α，已知产品尺寸服从正态分布N(μ，σ²)，其中参数σ²未知。

当H₀成立时，令

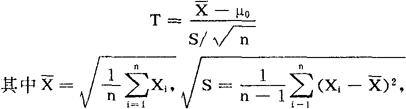
则统计量T服从n－1个自由度的t－分布。查t－分布表可得临界值t_α满足p｛｜T|＞t_α｝=α。如果通过样本算出的T满足｜T｜＞t_α，则拒绝H₀。否则认为样本与H₀无显着差异。

为解决各种不同问题而使用的各种各样的检验方法不胜枚举。归纳起来主要是参数检验与拟合优度检验两大类。

罗塔·萨克斯(Lothar Sachs)在他的《应用统计技术手册》(Applied statistics－A Handbook of Techniques)中对各种检验方法给出了比较详尽的介绍。