质点组的分析方法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第218页（1220字）

多个(有限或无限)相互关连的质点所组成的系统称为质点组。

质点组中质点间的相互作用力称为内力，质点组外的物体对质点组的作用力称为外力。在质点力学的基础上，对质点组的分析原则上没有什么困难，即采用所谓隔离法，写出质点组中每一质点的运动微分方程(每一质点有三个二阶微分方程)。值得指出的是，质点组中所含质点数愈多，这些方程数目也愈多，数字上亦就愈难求得精确解。实际上，至今也只是对一些特殊体系(如刚体及二体问题等)能求得精确解，其他则得求助于近似解法。

在分析质点组时，从基本定律出发可推知的一些一般推论常常是很有用的，它们分别是：

(1)质点组的动量定理，即质点组动量的时间变化率等于作用于质点组的诸外力的矢量和。由此还可推得质点组动量守恒定律，即质点组不受外力或合外力等于零时，体系的总动量守恒。

(2)质心运动定理 若有N个质点的质点组，其质心位置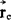定义为

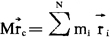
设质点组所受的诸外力分别为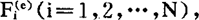则可推知

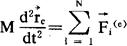
这表明质点组质心的运动犹如一个质点一样，此质点的质量等于整个质点组的质量和。其所受力就是质点组所受的合外力，此即质心运动定理。

(3)动量矩定理 质点i对某一点O的动量矩(又称角动量)定义为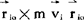是该点相对于O点的位置)，作用于i处的力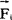对O点的力矩定义为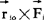，由力学基本定律可推知

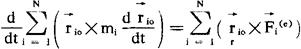
即质点组对O点的动量矩的时间变化率等于诸外力对O点的力矩的矢量和。由此易知一质点组动量矩守恒定律：质点组不受外力或虽受外力作用，但对O点合外力矩等于零时，则对O点的动量矩是一恒矢量。

并不难证明，对于质心C可有

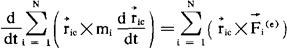
此即所谓质点组对质心的动量矩定理。

(4)动能定理 由基本定律出发可推知质点组的动能定理

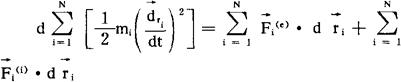
值得注意的是，此式右侧出现了各内力F_i⁽ⁱ⁾所作的元功除刚体外一般不为零。

故仅当质点组所受外力及内力均为保守力(或不作功)的情况下才能得到质点组的机械能守恒的形式

可以证明所谓柯希尼定理

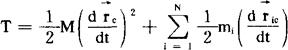
即质点组的总动能等于好似质量集中于质心的动能和各质点相对于质心的动能的总和。

还不难证明在质心参考系有