非线性规划

出处：按学科分类—经济 经济科学出版社《企业管理学大辞典》第557页（957字）

当目标函数或是约束条件中有至少一个是非线性函数时的规划问题为非线性规划。

非线性规划的形式为：

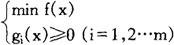
与线性规划不同，非线性规划并没有一个固定的解法，这是由于非线性规划可能的形式太多，如二次函数、指数函数和三角函数等等。非线性规划又可以划分不同的类型，针对其不同特点可采用不同的解法。

例：已知一段绳长1米，将这段绳围成一长方形，求如何围可使其面积最大?

解：设所围长方形长宽分别为x₁，x₂，则

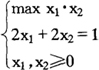
这就是一个简单的非线性规划模型。对于最简单的单变量非线性规划，如

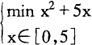
可以采用“爬山法”。做法是：在可行区域中任取一点(记为x₀)，向左或向右(随机决定)以一定步长迈出一步(记为x₁，设是向左走的，且步长为d，则x₁=x₀－d)。比较x₁与x₀处的目标函数值，若在x₁处较小，则表明走对了，下一步仍朝这个方向走一步，否则表明方向走反了，下步应朝另一个方向走一步。

这样无论初始点选在哪里，最终都能找到最优解。对比一下一个站在山腰上的人，他想走到峰顶，然而由于树木森森，他只能看到附近的地势，于是他将选择向高走一段，再观察哪儿更高以选择下一步的走向。

显然爬山者要能爬到山顶的话，他得确信这座山只有一个峰，否则他很有可能会走到矮的那个峰去了。爬山法以及其他一些求解一元非线性规划的方法是求解一般非线性规划问题的基础，其求解的效率对整个问题求解的效率影响很大。

如求解无约束非线性规划问题的最速下降法，其解法如下：先任取一个可行域中的点，按一定规则选取使目标函数下降最快的方向，在这个方向上寻找一点，使这一点的目标函数值最小，由于要找的点与初始点在一条已知的直线上，这时多元非线性规划问题就转化为求解一元非线性规划问题。总之，非线性规划的解法是试图将复杂的问题转化为简单的问题，再从简单的问题着手。